【题目】如图,在⊙O中,AB为直径,AC为弦,过点C作CD⊥AB于点D,将△ACD沿AC翻折,点D落在点E处,AE交⊙O于点F,连接OC、FC.
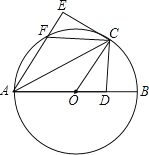
(1)求证:CE是⊙O的切线.
(2)若FC∥AB,求证:四边形AOCF是菱形.
参考答案:
【答案】见解析
【解析】
试题分析:(1)由翻折的性质可知∠FAC=∠OAC,∠E=∠ADC=90°,然后根据OA=OC得到∠OAC=∠OCA,从而得到OC∥AE,得到∠OCE=90°,从而判定切线.
(2)利用FC∥AB,OC∥AF判定四边形AOCF是平行四边形,根据OA=OC,利用邻边相等的平行四边形是菱形判定□AOCF是菱形.
(1)证明:由翻折可知∠FAC=∠OAC,∠E=∠ADC=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC∥AE
∴∠OCE=90°,
即OC⊥CE,
∵OC是⊙O的半径
∴CE是⊙O的切线;
(2)证明:∵FC∥AB,OC∥AF,
∴四边形AOCF是平行四边形,
∵OA=OC,
∴平行四边形AOCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面等式成立的是( )
A.83.5°=83°50′
B.37°12′36″=37.48°
C.24°24′24″=24.44°
D.41.25°=41°15′
-
科目: 来源: 题型:
查看答案和解析>>【题目】直五棱柱的底面是 边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中有一张三角形纸片AOB,其顶点A,B的坐标分别为A(﹣6,0),B(0,8),点O为坐标原点.

(1)求边AB的长;
(2)点C是线段OB上一点,沿线段AC所在直线折叠△AOB,使得点O落在边AB上的点D处,求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】O为直线DA上一点,OB⊥OF,EO是∠AOB的平分线.
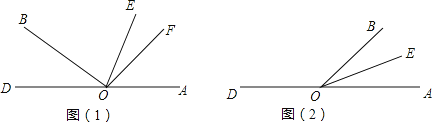
(1)如图(1),若∠AOB=130°,求∠EOF的度数;
(2)若∠AOB=α,90°<α<180°,求∠EOF的度数;
(3)若∠AOB=α,0°<α<90°,请在图(2)中画出射线OF,使得(2)中∠EOF的结果仍然成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个角的补角是这个角的余角的3倍,则这个角的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+6分别交x轴、y轴于A、B两点,抛物线y=﹣
x+6分别交x轴、y轴于A、B两点,抛物线y=﹣ x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.
x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.
(1)点A的坐标为 ,点D的坐标为 ;
(2)探究发现:
①假设P与点D重合,则PB+PC= ;(直接填写答案)
②试判断:对于任意一点P,PB+PC的值是否为定值?并说明理由;
(3)试判断△PAB的面积是否存在最大值?若存在,求出最大值,并求出此时点P的坐标;若不存在,说明理由.
相关试题

