搜索
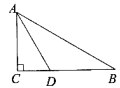
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD为∠CAB的角平分线,若CD=3，则DB=____.
参考答案：
【答案】6
【解析】
先根据三角形的内角和定理，求出∠BAC的度数=180°﹣90°﹣30°=60°，然后利用角平分线的性质，求出∠CAD的度数
∠BAC=30°．在Rt△ACD中，根据30°角所对的直角边等于斜边的一半，即可求出AD的长，进而得出BD．
在Rt△ABC中∠C=90°，∠B=30°，∴∠BAC=180°﹣90°﹣30°=60°．
∵AD是角平分线，∴∠BAD=∠CAD∠BAC=30°．在Rt△ACD中，∵∠CAD=30°，CD=3，∴AD=6．
∵∠B=∠BAD=30°，∴BD=AD=6．
故答案为：6．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校在五一期间组织学生外出旅游，如果单独租用45座的客车若干辆，恰好坐满；如果单独租用60座的客车，可少租一辆，并且余30个座位．
(1)求外出旅游的学生人数是多少，单租45座的客车需多少辆？
(2)已知45座的客车每辆租金250元，60座的客车每辆租金300元，为节省租金，并且保证每个学生都有座，决定同时租用两种客车，使得租车总数比单租45座的客车少一辆，问45座的客车和60座的客车分别租多少辆才能使得租金最少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】黄石市在创建国家级文明卫生城市中，绿化档次不断提升．某校计划购进A，B两种树木共100棵进行校园绿化升级，经市场调查：购买A种树木2棵，B种树木5棵，共需600元；购买A种树木3棵，B种树木1棵，共需380元．
（1）求A种，B种树木每棵各多少元？
（2）因布局需要，购买A种树木的数量不少于B种树木数量的3倍．学校与中标公司签订的合同中规定：在市场价格不变的情况下（不考虑其他因素），实际付款总金额按市场价九折优惠，请设计一种购买树木的方案，使实际所花费用最省，并求出最省的费用．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如下图所示，D为BC上一点，且AB=AC=BD，则图中∠1与∠2的关系是（ ）
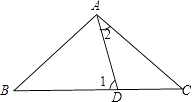
A.∠1=2∠2
B.∠1+∠2=180°
C.∠1+3∠2=180°
D.3∠1﹣∠2=180° -
科目： 来源： 题型：
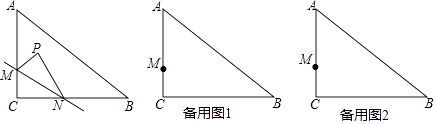
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点M在AC边上，点N从点C出发沿折线CB﹣BA运动到点A停止，点P是点C关于直线MN的对称点，连接MP，NP（当点N与点C，A重合时，点P均与点C重合）．
（1）若CM=2，
①又当点N在CB上，MP∥BC时，则CN= ， MN=；
（2）在（1）的条件下，求点P到AB边的距离的最小值，并求出当取得这个最小值时，点P运动路线的长是多少？（参考数据：sin54°=cos36°≈
，sin36°=cos54°≈ 
，结果保留π）
（3）设MC=a（a＞2），其他条件不变，当有且只能有唯一的点P落在线段AB上时，直接写出a的取值范围 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂有甲种原料130kg，乙种原料144kg．现用这两种原料生产出A，B两种产品共30件．已知生产每件A产品需甲种原料5kg，乙种原料4kg，且每件A产品可获利700元；生产每件B产品需甲种原料3kg，乙种原料6kg，且每件B产品可获利900元．设生产A产品x件（产品件数为整数件），根据以上信息解答下列问题：
（1）生产A，B两种产品的方案有哪几种；
（2）设生产这30件产品可获利y元，写出y关于x的函数解析式，写出（1）中利润最大的方案，并求出最大利润．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（观察）方程
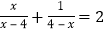的解是
的解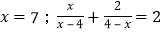是
；
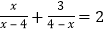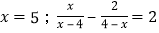的解是
的解是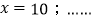
（发现）根据你的阅读回答问题：
（1）
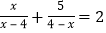的解为_______；（2）关于
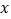的方程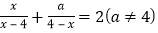
的解为_______(用含
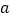的代数式表示)，并利用“方程的解的概念”验证．（类比）
（3）关于
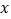的方程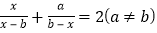
的解为_________(用含
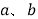的代数式表示)．
相关试题
