【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点,与y轴交于点C,顶点为D,抛物线的对称轴DF与BC相交于点E,与x轴相交于点F.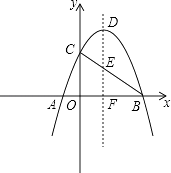
(1)求线段DE的长;
(2)设过E的直线与抛物线相交于点M(x1 , y1),N(x2 , y2),试判断当|x1﹣x2|的值最小时,直线MN与x轴的位置关系,并说明理由;
(3)设P为x轴上的一点,∠DAO+∠DPO=∠α,当tan∠α=4时,求点P的坐标.
参考答案:
【答案】
(1)
解:由抛物线y=﹣x2+2x+3可知,C(0,3),
令y=0,则﹣x2+2x+3=0,解得:x=﹣1,x=3,
∴A(﹣1,0),B(3,0);
∴顶点x=1,y=4,即D(1,4);
∴DF=4
设直线BC的解析式为y=kx+b,代入B(3,0),C(0,3)得;
![]() ,解得
,解得 ![]() ,
,
∴解析式为;y=﹣x+3,
当x=1时,y=﹣1+3=2,
∴E(1,2),
∴EF=2,
∴DE=DF﹣EF=4﹣2=2.
(2)
解:设直线MN的解析式为y=kx+b,
∵E(1,2),
∴2=k+b,
∴k=2﹣b,
∴直线MN的解析式y=(2﹣b)x+b,
∵点M、N的坐标是 ![]() 的解,
的解,
整理得:x2﹣bx+b﹣3=0,
∴x1+x2=b,x1x2=b﹣3;
∵|x1﹣x2|= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴当b=2时,|x1﹣x2|最小值=2 ![]() ,
,
∵b=2时,y=(2﹣b)x+b=2,
∴直线MN∥x轴.
(3)
解:如图2,∵D(1,4),
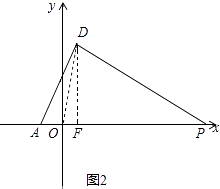
∴tan∠DOF=4,
又∵tan∠α=4,
∴∠DOF=∠α,
∵∠DOF=∠DAO+∠ADO=∠α,
∵∠DAO+∠DPO=∠α,
∴∠DPO=∠ADO,
∴△ADP∽△AOD,
∴AD2=AOAP,
∵AF=2,DF=4,
∴AD2=AF2+DF2=20,
∴OP=19,
同理,当点P在原点左侧,OP=17.
∴P1(19,0),P2(﹣17,0).
【解析】(1)根据抛物线的解析式即可求得与坐标轴的坐标及顶点坐标,进而求得直线BC的解析式,把对称轴代入直线BC的解析式即可求得.(2)设直线MN的解析式为y=kx+b,依据E(1,2)的坐标即可表示出直线MN的解析式y=(2﹣b)x+b,根据直线MN的解析式和抛物线的解析式即可求得x2﹣bx+b﹣3=0,所以x1+x2=b,x1 x2=b﹣3;根据完全平方公式即可求得∵|x1﹣x2|= ![]() =
= ![]() =
= ![]() =
= ![]() ,所以当b=2时,|x1﹣x2|最小值=2
,所以当b=2时,|x1﹣x2|最小值=2 ![]() ,因为b=2时,y=(2﹣b)x+b=2,所以直线MN∥x轴.(3)由D(1,4),则tan∠DOF=4,得出∠DOF=∠α,然后根据三角形外角的性质即可求得∠DPO=∠ADO,进而求得△ADP∽△AOD,得出AD2=AOAP,从而求得OP的长,进而求得P点坐标.
,因为b=2时,y=(2﹣b)x+b=2,所以直线MN∥x轴.(3)由D(1,4),则tan∠DOF=4,得出∠DOF=∠α,然后根据三角形外角的性质即可求得∠DPO=∠ADO,进而求得△ADP∽△AOD,得出AD2=AOAP,从而求得OP的长,进而求得P点坐标.
【考点精析】本题主要考查了二次函数的图象和两点间的距离的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.
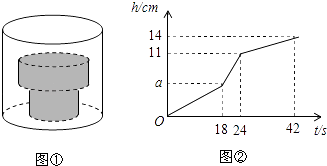
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为cm,匀速注水的水流速度为cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2 , 求“几何体”上方圆柱的高和底面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.
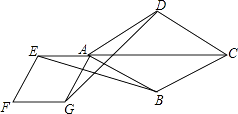
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=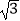 ,求GD的长.
,求GD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,AD=4,E为AB上一点,AE=1,M为射线AD上一动点,AM=a(a为大于0的常数),直线EM与直线CD交于点F,过点M作MG⊥EM,交直线BC于点G.

(1)若M为边AD中点,求证△EFG是等腰三角形;
(2)若点G与点C重合,求线段MG的长;
(3)请用含a的代数式表示△EFG的面积S,并指出S的最小整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )

A.( ,3)、(﹣
,3)、(﹣  ,4)
,4)
B.( ,3)、(﹣
,3)、(﹣  ,4)??
,4)??
C.( ,
,  )、(﹣
)、(﹣  ,4)
,4)
D.( ,
,  )、(﹣
)、(﹣  ,4)
,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地. 如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.
下几种说法:
①货车的速度为60千米/小时;
②轿车与货车相遇时,货车恰好从甲地出发了3. 9小时;
③若轿车到达乙地后,马上沿原路以CD段速度返回,则轿车从乙地出发
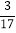 小时再次与货车相遇;
小时再次与货车相遇;其中正确的个数是_________. (填写序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
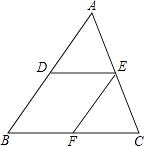
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
相关试题

