搜索
【题目】在Rt△ABC中，∠C＝90°，两锐角的度数之比为2：1，其最短边为1，射线CP交AB所在的直线于点P，且∠ACP＝30°，则线段CP的长为_____．
参考答案：
【答案】
或1
【解析】
先根据题意得出两个锐角的度数，再分两种情况：（1）∠A＝60°，∠B＝30°，CA＝1；（2）∠A＝30°，∠B＝60°，CB＝1．分别画图并求解即可．
∵在Rt△ABC中，∠C＝90°，两锐角的度数之比为2：1
∴两锐角的度数为：60°，30°.
分两种情况：（1）∠A＝60°，∠B＝30°，CA＝1,
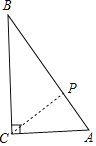
∵∠ACP＝30°，
∴∠APC＝90°，
∴PA＝
，
∴CP＝
＝ ；
（2）∠A＝30°，∠B＝60°，CB＝1，
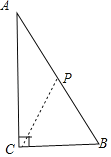
∵∠ACP＝30°，
∴∠BCP＝60°，
又∵∠B＝60°，
∴△BCP为等边三角形，
∴CP＝CB＝1.
故答案为：或1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（ ）
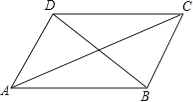
A.①②B.②③C.①③D.②④
-
科目： 来源： 题型：
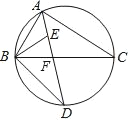
查看答案和解析>>【题目】如图，∠BAC的平分线交AABC的外接圆于点D，交BC于点F，∠ABC的平分线交AD于点E．
（1）求证：DE=DB.
（2）若∠BAC=90°，BD=4，求△ABC外接圆的半径；
（3）若BD=6，DF=4，求AD的长
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知矩形ABCD沿着直线BD折叠，使点C落在C/处，BC/交AD于E，AD=8，AB=4，DE的长=________________．
-
科目： 来源： 题型：
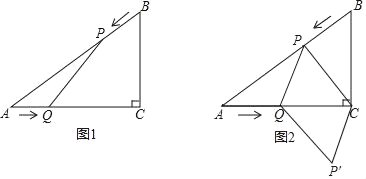
查看答案和解析>>【题目】已知：如图1在Rt△ABC中，∠C=90°，AC=8cm，BC=6cm，点P由点B出发沿BA方向向点A匀速运动，速度为2cm/s；同时点Q由点A出发沿AC方向点C匀速运动，速度为lcm/s；连接PQ，设运动的时间为t秒（0＜t＜5），解答下列问题：
（1）当为t何值时，PQ∥BC；
（2）设△AQP的面积为y（cm2），求y关于t的函数关系式，并求出y的最大值；
（3）如图2，连接PC，并把△PQC沿QC翻折，得到四边形PQPC，是否存在某时刻t，使四边形PQP'C为菱形？若存在，求出此时t的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3．在Rt△ABC的外部拼接一个合适的直角三角形，使得拼成的图形是一个等腰三角形，如图所示．要求：在答题卡的两个备用图中分别画出两种与示例不同的拼接方法，并在图中标明拼接的直角三角形的三边长．（请同学们先用铅笔画出草图，确定后再用0.5毫米的黑色签字笔画出正确的图形）
-
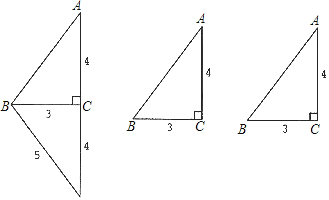
科目： 来源： 题型：
查看答案和解析>>【题目】现场学习题：问题背景：在△ABC中，AB、BC、AC三边的长分别为
、
、
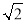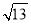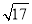，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你将△ABC的面积直接填写在横线上．
思维拓展：（2）我们把上述求△ABC面积的方法叫做构图法．若△ABC三边的长分别为
、
、
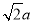（a＞0），请利用图2的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积是： ．
相关试题
