【题目】如图,直角坐标系中,△ABC的三个顶点的坐标分别为(2,1),(﹣1,3),(﹣3,2).
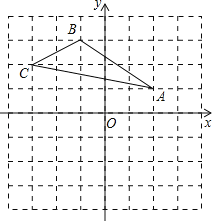
(1)在图中作出△ABC关于x轴对称的△A′B′C′,并写出点A′的坐标为 ,点B的坐标为 ,点C′的坐标为 ;
(2)求△ABC的面积;
(3)若点P(a,a﹣2)与点Q关于y轴对称,若PQ=8,求点P的坐标.
参考答案:
【答案】(1)见解析,A′(2,﹣1),B′(﹣1,﹣3),C′(﹣3,﹣2);(2)3.5;(3)点P的坐标为(4,2)或(﹣4,﹣6).
【解析】
(1)根据关于x轴对称的点的坐标特征,横坐标相反,纵坐标相同即可求得对应点的坐标.
(2)根据割补法将求△ABC的面积问题转化为求其它图形的面积和或面积差问题.
(3)根据关于y轴对称的点的坐标特征,横坐标相反,纵坐标相同将Q点的坐标用a表示出来,然后列出线段PQ的长的关系式,求解即可.
解:
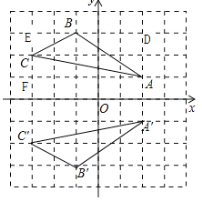
(1)如图,△A′B′C′为所作;
A′(2,﹣1),B′(﹣1,﹣3),C′(﹣3,﹣2);
(2)![]()
=![]()
=3.5
(3)∵点P(a,a﹣2)与点Q关于y轴对称,
∴Q(﹣a,a﹣2),
∵PQ=8,
∴|a﹣(﹣a)|=8,
解得a=4或a=﹣4,
∴点P的坐标为(4,2)或(﹣4,﹣6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠CAB=36°,以C为原点,C所在直线为y轴,BC所在直线为x轴建立平面直角坐标系 ,在坐标轴上取一点M使△MAB 为等腰三角形,符合条件的 M 点有( )

A.6个B.7个
C.8个D.9个
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年本市蜜桔大丰收,某水果商销售一种蜜桔,成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
(销售利润=销售价-成本价)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于 x 的方程 2x2+kx﹣1=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣1,求另一个根及 k 值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知在△ABC中,∠ACB=90°,AC=BC=1,点D是AB上任意一点,AE⊥AB,且AE=BD,DE与AC相交于点F.
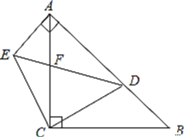
(1)试判断△CDE的形状,并说明理由.
(2)是否存在点D,使AE=AF?如果存在,求出此时AD的长,如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2+6x+5=0 (配方法)
(2)x2﹣1=2(x+1)(因式分解法)
(3)2x2+3=6x (公式法)
相关试题

