【题目】如图,在![]() 中,
中,![]() 的垂直平分线交
的垂直平分线交![]() 边于点
边于点![]() 的垂 直平分线交
的垂 直平分线交![]() 边于点
边于点![]() .
.
![]() 求
求![]() 的周长.
的周长.
![]() 求
求![]() 的度数.
的度数.
![]() 判断△AEN 的形状并证明.
判断△AEN 的形状并证明.

参考答案:
【答案】(1)12;(2)60°;(3)△AEN为等边三角形,理由见详解.
【解析】
(1)根据题意,利用线段垂直平分线性质得到AE=BE,AN=CN,等量代换即可确定出三角形AEN周长;
(2)由等边对等角,以及三角形内角和定理求出所求角度数即可;
(3)根据题意利用外角性质确定出三角形AEN三个角都为60°,即可确定出三角形形状.
解:(1)∵AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,
∴AE=BE,AN=CN,
∵BC=12,
∴△AEN周长l=AE+EN+AN=BE+EN+NC=BC=12;
(2)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AE=BE,AN=CN,
∴∠BAE=∠CAN=30°,
∴∠EAN=∠BAC-∠BAE-∠CAN=60°;
(3)△AEN为等边三角形,理由如下:
∵∠AEN=∠B+∠BAE=60°,∠ANE=∠C+∠CAN=60°,
∴△AEN为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校长暑假将带领该校前级“三好学生”去北京大学游学,甲旅行社说:如果校长买全票一 张,则其余的学生可享受半价优惠.乙旅行社说:“包括校长在内全部按票价的六折优惠”. 若全票价为
 元,两家旅行社的服务质量相同,根据三好学生的人数你认为选择哪一 家旅行社才会比较合算?
元,两家旅行社的服务质量相同,根据三好学生的人数你认为选择哪一 家旅行社才会比较合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数y=
 (k>1)和y=
(k>1)和y= 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y= 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y= 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y= 的图象于点B,BE⊥x轴于点E,当点P在y=
的图象于点B,BE⊥x轴于点E,当点P在y= 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AD是⊙O直径,过点A的切线与CB的延长线交于点E.
(1)求证:EA2=EBEC;
(2)若EA=AC,cos∠EAB=
 ,AE=12,求⊙O的半径.
,AE=12,求⊙O的半径.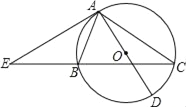
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题: 同学们,我们把学习新的数学知识的时候,经常利用“化归“的数学思想方法解决问题,比如,我们在学习二元一次方程组的解法时,是通过“消元”的方法将二元方程化归成我们所 熟悉的一元方程,从而正确求解.下面我们就利用“化归”的数学方法解决新的问题. 首先,我们把像这样,只含有一个未知数,并且未知教的最高次数是
 的不等式,称为一元二次不等式.通过以前的学习,我们已经认识了一无一次不等式、一元一次不等式组并掌握 了它们的解法.同学们,你们能类比一元一次不等式(组)的解法求出一元二次不等式的解 集吗? 例题:解一元二次不等式
的不等式,称为一元二次不等式.通过以前的学习,我们已经认识了一无一次不等式、一元一次不等式组并掌握 了它们的解法.同学们,你们能类比一元一次不等式(组)的解法求出一元二次不等式的解 集吗? 例题:解一元二次不等式 为了解决这个问题,我们需要将一元二次不等式“化归”到一元一次不等式(组),通过平方差公式的逆用,我们可以把
为了解决这个问题,我们需要将一元二次不等式“化归”到一元一次不等式(组),通过平方差公式的逆用,我们可以把 写成
写成 的形式,从面将
的形式,从面将 转化为
转化为 ,然后再利用两数相乘的符号性质将一元二次不等式转化成一元一次不等式(组),从而解决问题.
,然后再利用两数相乘的符号性质将一元二次不等式转化成一元一次不等式(组),从而解决问题.解:

 可化为
可化为
由有理数的乘法法则“两数相乘,同号得正”,得①
 ②
②
解不等式组①,
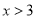
解不等式组②,

即一元二次不等式
 的解集为
的解集为
拓展应用:
 求一元二次不等式
求一元二次不等式 的解集.
的解集. 求分式不等式
求分式不等式 的解集.
的解集. 求一元二次不等式
求一元二次不等式 的解集.
的解集.
相关试题

