【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补. 
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH; 
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由. 
参考答案:
【答案】
(1)解:如图1,∵∠1与∠2互补,
∴∠1+∠2=180°.
又∵∠1=∠AEF,∠2=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD
(2)解:如图2,由(1)知,AB∥CD,
∴∠BEF+∠EFD=180°.
又∵∠BEF与∠EFD的角平分线交于点P,
∴∠FEP+∠EFP= ![]() (∠BEF+∠EFD)=90°,
(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF.
∵GH⊥EG,
∴PF∥GH
(3)解:∠HPQ的大小不发生变化,理由如下:
如图3,∵∠1=∠2,
∴∠3=2∠2.
又∵GH⊥EG,
∴∠4=90°﹣∠3=90°﹣2∠2.
∴∠EPK=180°﹣∠4=90°+2∠2.
∵PQ平分∠EPK,
∴∠QPK= ![]() ∠EPK=45°+∠2.
∠EPK=45°+∠2.
∴∠HPQ=∠QPK﹣∠2=45°,
∴∠HPQ的大小不发生变化,一直是45°.

【解析】(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF、∠CFE互补,所以易证AB∥CD;(2)利用(1)中平行线的性质推知°;然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG⊥PF,故结合已知条件GH⊥EG,易证PF∥GH;(3)利用三角形外角定理、三角形内角和定理求得∠4=90°﹣∠3=90°﹣2∠2;然后由邻补角的定义、角平分线的定义推知∠QPK= ![]() ∠EPK=45°+∠2;最后根据图形中的角与角间的和差关系求得∠HPQ的大小不变,是定值45°.
∠EPK=45°+∠2;最后根据图形中的角与角间的和差关系求得∠HPQ的大小不变,是定值45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我区注重城市绿化提高市民生活质量,新建林荫公园计划购买甲、乙两种树苗共800株,甲种树苗每株12元,乙种树苗每株15元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.
(1)若购买这两种树苗共用去10500元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x+1)(x+q)的结果中不含x的一次项,则常数q= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以正方形ABCD的对角线BD为边作菱形BDEF,当点A,E,F在同一直线上时,∠F的正切值为___________.
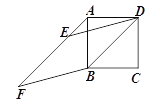
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为( )
A.y=x+2
B.y=﹣x+2
C.y=x+2或y=﹣x+2
D.y=﹣x+2或y=x﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
(1)从运动开始,当t取何值时,PQ∥CD?
(2)从运动开始,当t取何值时,△PQC为直角三角形?
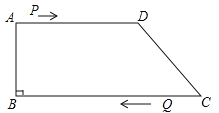
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x、y的二元一次方程组
 的解都为正数.
的解都为正数.
(1)求a的取值范围;
(2)化简|a+1|﹣|a﹣1|;
(3)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求a的值.
相关试题

