搜索
【题目】如图是一个组合烟花的横截面，其中16个圆的半径相同，点A、B、C、D分别是四个角上的圆的圆心，且四边形ABCD为正方形．若圆的半径为r，组合烟花的高为h，则组合烟花侧面包装纸的面积至少需要（接缝面积不计）（ ）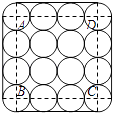 
A.26πrh
B.24rh+πrh
C.12rh+2πrh
D.24rh+2πrh
参考答案：
【答案】D
【解析】解：由图形知，正方形ABCD的边长为6r， ∴其周长为4×6r=24r，
∵一个圆的周长为：2πr，
∴截面的周长为：24r+2πr，
∴组合烟花的侧面包装纸的面积为：（24r+2πr）h=24rh+2πrh．
故选D．
【考点精析】认真审题，首先需要了解相切两圆的性质(如果两圆相切，那么切点一定在连心线上，它们是轴对称图形，对称轴是两圆的连心线)，还要掌握扇形面积计算公式(在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）)的相关知识才是答题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】建立模型：
如图1，已知△ABC，AC=BC，∠C=90°，顶点C在直线l上．
操作：
过点A作AD⊥l于点D，过点B作BE⊥l于点E．求证：△CAD≌△BCE．
模型应用：
（1）如图2，在直角坐标系中，直线l1：y=
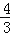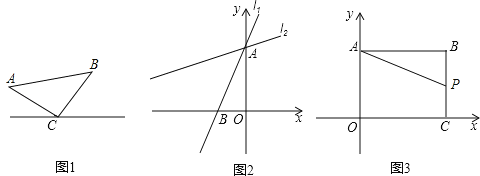
x+4与y轴交于点A，与x轴交于点B，将直线l1绕着点A顺时针旋转45°得到l2．求l2的函数表达式．（2）如图3，在直角坐标系中，点B（8，6），作BA⊥y轴于点A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，2a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国是一个严重缺水的国家．为了加强公民的节水意识，某市制定了如下用水收费标准：每户每月的用水不超过6吨时，水价为每吨2元，超过6吨时，超过的部分按每吨3元收费．该市某户居民5月份用水x吨，应交水费y元．
（1）若0＜x≤6，请写出y与x的函数关系式．
（2）若x＞6，请写出y与x的函数关系式．
（3）如果该户居民这个月交水费27元，那么这个月该户用了多少吨水？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（－3，5），B（－2，1），C（－1，3）．
（1）画出△ABC关于x轴的对称图形△A1B1C1；
（2）画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2；
（3）如果AC上有一点M（a，b）经过上述两次变换，那么对应A2C2上的点M2的坐标是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，CD是⊙O的直径，弦AB⊥CD，垂足为点M，AB=20，分别以CM、DM为直径作两个大小不同的 ⊙O1和⊙O2 ， 则图中阴影部分的面积为（结果保留π）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形草坪ABCD中，∠B=90°，AB=24m，BC=7m，CD=15m，AD=20m.
（1）判断∠ADC是否是直角，并说明理由；
（2）试求四边形草坪ABCD的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面的解题过程：
计算：（－15）÷（
－1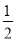
－3）×6.解：原式＝（－15）÷（－
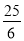）×6（第一步）＝（－15）÷（－25）（第二步）
＝
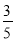.（第三步）解答：（1）上面解题过程，从第____步开始错误，错误的原因是_____.
（2）请写出正确的解题过程．
相关试题
