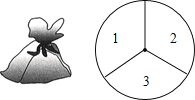
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).
(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
参考答案:
【答案】(1)![]() ;(2)游戏公平
;(2)游戏公平
【解析】
试题分析:(1)因为口袋中有4个小球,大于2的有两个分别是3,4,由此可求出其概率.
(2)游戏公平,分别求出题目各自获胜的概率,比较概率是否相等,即可判定游戏是否公平.
解:(1)∵的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,
∴从口袋中摸出一个小球,所摸球上的数字大于2的概率为![]() ;
;
故答案为:![]() ;
;
(2)游戏公平.
列举所有等可能的结果12个:
1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
∴所摸球上的数字与圆盘上转出数字之和小于5的概率为P=![]() ,
,
∴游戏公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.
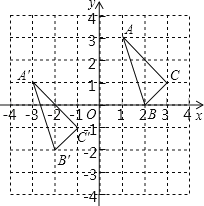
(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
-
科目: 来源: 题型:
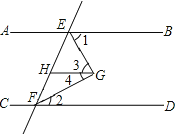
查看答案和解析>>【题目】已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
求证:∠EGF=90°
(1)把下列证明过程及理由补充完整.
(2 )请你用精炼准确的文字将上述结论总结出来.
证明:∵HG∥AB(已知)
∴∠1=∠3 ( )
又∵HG∥CD(已知)
∴∠2=∠4(同理)
∵AB∥CD(已知)
∴∠BEF+ =180° ( )
又∵EG平分∠BEF(已知)
∴∠1=
 ∠
∠ 又∵FG平分∠EFD(已知)
∴∠2=
 ∠EFD (同理)
∠EFD (同理)∴∠1+∠2=
 ( + )
( + )∴∠1+∠2=90°
∴∠3+∠4=90°
即∠EGF=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是( )

A.△AED≌△BFA B.DE-BF=EF C.△BGF∽△DAE D.DE-BG=FG
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2个单位长度到点A′处,则点A′的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一元二次方程(x+1)(1﹣x)=2x化成二次项系数大于零的一般式是 , 其中二次项系数是 , 一次项的系数是 , 常数项是;
-
科目: 来源: 题型:
查看答案和解析>>【题目】圣诞节到了,商店进行打折促销活动.妈妈以八折的优惠购买了一件运动服,节省28元,那么妈妈购买这件衣服实际花费了元.
相关试题

