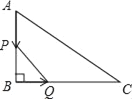
【题目】如图,在△ABC中,∠B=90°,BC=8cm,AC=10cm,动点A从点A出发以1cm/s的速度沿AB边运动,同时动点Q从点B出发以2cm/s的速度沿BC边运动.设运动时间为t秒.
(1)若△PBQ的面积等于8cm2,求t的值;
(2)若PQ的长等于![]() cm,求t的值.
cm,求t的值.
参考答案:
【答案】(1)当P、Q经过2或4秒时,△PBQ的面积为8cm2;(2)当t为1或![]() 时,PQ的长等于
时,PQ的长等于![]() cm.
cm.
【解析】分析:(1)由题意,利用勾股定理求得AB=6,可设P、Q经过t秒,使△PBQ的面积为8cm2,则PB=6﹣t,BQ=2t,根据三角形面积的计算公式,S△PBQ=![]() BQPB,列出方程,解答出即可;
BQPB,列出方程,解答出即可;
(2)可设P、Q两点运动t秒时,则PB=6﹣t,BQ=2t,根据勾股定理,可得PQ2=BP2+BQ2,代入整理即可求出.
详解:(1)AB=![]() =6,设P、Q经过t秒时,△PBQ的面积为8cm2,则PB=6﹣t,BQ=2t.
=6,设P、Q经过t秒时,△PBQ的面积为8cm2,则PB=6﹣t,BQ=2t.
∵∠B=90°,AB=6cm,BC=8cm,∴,![]() (6﹣t)2t=8,解得:t1=2,t2=4.
(6﹣t)2t=8,解得:t1=2,t2=4.
答:当P、Q经过2或4秒时,△PBQ的面积为8cm2;
(2)设P、Q两点运动t秒时,PQ的长等于![]() cm,则29=(6﹣t)2+(2t)2,解得:t1=1,t2=
cm,则29=(6﹣t)2+(2t)2,解得:t1=1,t2=![]() .
.
答:当t为1或![]() 时,PQ的长等于
时,PQ的长等于![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长城汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润45万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)

(2)

(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=10cm,BC=16cm,现点P从点B出发,沿BC向C点运动,运动速度为
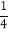 m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值可能是_____.
m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值可能是_____.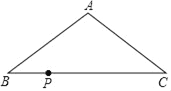
-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=﹣c,b=2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=nx2+x,函数y1+y2恰是y1﹣y2的“反倍顶二次函数”,求n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACB=120°,以AC、BC为边向外作等边△ACF和等边△BCF,点P、M、N分别为AB、CF、CE的中点
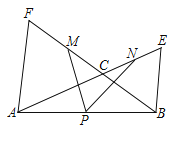
(1) 求证:PM=PN
(2) 求证:
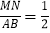
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

相关试题

