Question

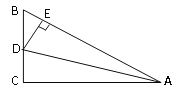
【题目】如图，在等边三角形ABC中，BD⊥AC于D，延长BC到E，使CE=CD，AB=6cm．
（1）求BE的长；
（2）判断△BDE的形状，并说明理由．

Answer 1

【答案】（1）9；（2）△BDE为等腰三角形．理由见解析.

【解析】试题分析：（1）根据等边三角形的性质得BC=AB=6cm，再根据“三线合一”得AD=CD= AC=3cm，而CD=CE=3cm，所以BE=BC+CE=9cm；
（2）根据等边三角形的性质得∠ABC=∠ACB=60°，再根据“三线合一”得∠CBD=∠ABC=30°，而CD=CE，则∠CDE=∠E，接着利用三角形外角性质得∠CDE+∠E=∠ACB=60°，所以∠E=30°，于是得到∠CBD=∠E，然后根据等腰三角形的判定即可得到△BDE为等腰三角形．

试题解析：

（1）∵△ABC为等边三角形，
∴BC=AB=6cm，
∵BD⊥AC，
∴AD=CD= AC=3cm，
∵CD=CE=3cm，
∴BE=BC+CE=6cm+3cm=9cm； ..........3分
（2）△BDE为等腰三角形．理由如下：
∵△ABC为等边三角形，
∴∠ABC=∠ACB=60°，
∵BD⊥AC，
∴∠CBD=∠ABC=30°，
∵CD=CE，
∴∠CDE=∠E，
而∠CDE+∠E=∠ACB=60°，
∴∠E=30°，
∴∠CBD=∠E，
∴△BDE为等腰三角形