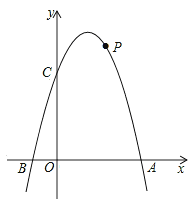
【题目】如图,已知二次函数y=﹣x2+bx+c的图象交x轴于点A(4,0)和点B,交y轴于点C(0,4).
(1)求这个二次函数的表达式;
(2)若点P在第一象限内的抛物线上,求四边形AOCP面积的最大值和此时点P的坐标;
(3)在平面直角坐标系内,是否存在点Q,使A,B,C,Q四点构成平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
参考答案:
【答案】(1)y=﹣x2+3x+4;(2)P(2,6),16;(3)存在,Q的坐标为(﹣5,4)或(5,4)或(3,﹣4)
【解析】试题分析:(1)、将点A和点C的坐标代入解析式,从而求出b和c的值,然后得出函数解析式;(2)、根据二次函数得出点B的坐标,根据题意可得要使△ACP的面积达到最大时,经过点P且与AC的平行直线与抛物线只有一个交点,从而得出答案;(3)、分两种情况来进行讨论:①以AB为边时,CQ∥AB,CQ=AB 过点C作平行于AB的直线l,设点Q的坐标为(d,4),则CQ=|d|,根据题意得出AB=5,从而得出d的值,得出点Q的坐标;②、以AB为对角线时,CQ必过线段AB中点,且被AB平分,即:AB的中点也是CQ的中点,根据题意得出中点的坐标,得出直线CQ的解析式,设出点Q的坐标,然后根据勾股定理求出点Q的坐标得出答案.
试题解析:(1)∵二次函数y=﹣x2+bx+c的图象交x轴于点A(4,0)和点B,交y轴于点C(0,4).
∴![]() ,∴
,∴![]() , ∴二次函数的表达式为y=﹣x2+3x+4,
, ∴二次函数的表达式为y=﹣x2+3x+4,
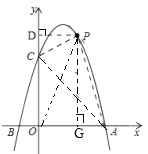
(2)如图,

由(1)有,二次函数的表达式为y=﹣x2+3x+4, 令y=0,得x=4,或x=-1,∴B(-1,0)
连接AC,PA,PC,要使四边形![]() 的面积最大,当且仅当
的面积最大,当且仅当![]() 的面积最大时,
的面积最大时,
∴点P在平行于直线AC,且该直线与抛物线只有一个交点时,S△PAC最大,
即:S四边形AOCP最大;
∵A(4,0),C(0,4), ∴直线AC解析式为![]() ,
,
设与直线AC平行的直线解析式为![]() ,则
,则
![]() ,∴
,∴ ![]()
∴![]() ,∴
,∴![]() ,∴点P(2,6),
,∴点P(2,6),
连接PO,过点P作PD⊥y轴,PG⊥x轴,则PD=2,PG=6,
∴![]() .
.
(3)存在点Q,使A,B,C,Q四点构成平行四边形,
p>理由:①以AB为边时,CQ∥AB,CQ=AB 过点C作平行于AB的直线l,∵C(0,4),∴直线l解析式为y=4,∴点Q在直线l上, 设Q(d,4),∴CQ=|d|,
∵A(﹣4,0),B(1,0),∴AB=5,∴|d|=5,∴d=±5, ∴Q(﹣5,4)或(5,4),
②以AB为对角线时,CQ必过线段AB中点,且被AB平分,即:AB的中点也是CQ的中点,
∵A(4,0),B(-1,0),∴线段AB中点坐标为(![]() ,0),
,0),
∵C(0,4),∴直线CQ解析式为y=-![]() x+4,设点Q(m,-
x+4,设点Q(m,-![]() m+4),
m+4),
∴ ,∴m=0(舍)或m=3,∴Q(3,﹣4),
,∴m=0(舍)或m=3,∴Q(3,﹣4),
即:满足条件的点Q的坐标为(﹣5,4)或(5,4)或(3,﹣4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣3,2,0,﹣0.5四个数中,比﹣1小的数是( )
A. ﹣3 B. 2 C. 0 D. ﹣0.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=
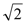 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②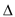 AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )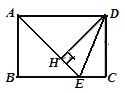
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
-
科目: 来源: 题型:
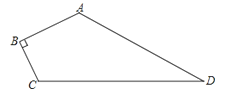
查看答案和解析>>【题目】一块试验田的形状如图,已知:∠ABC=90°,AB=4m,BC=3m,AD=12m,CD=13m.求这块试验田的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学为了进一步普及卫生知识、提高卫生意识、推广健康生活,今年3月份举行了一次卫生知识竞赛,这次竞赛中共有20道题,每一题答对得5分,答错或不答都扣3分.
(1)小明考了68分,那么小明答对了多少道题?
(2)小亮获得二等奖(70分~90分),请你算算小亮答对了几道题? -
科目: 来源: 题型:
查看答案和解析>>【题目】新能源汽车节能、环保,越来越受消费者喜爱,各种品牌相继投放市场,我国新能源汽车近几年销量全球第一,2016年销量为50.7万辆,销量逐年增加,到2018年销量为125.6万辆.设年平均增长率为x,可列方程为( )
A. 50.7(1+x)2=125.6B. 125.6(1﹣x)2=50.7
C. 50.7(1+2x)=125.6D. 50.7(1+x2)=125.6
相关试题

