【题目】已知反比例函数y=![]() (a为常数)的图象经过点B(﹣4,2).
(a为常数)的图象经过点B(﹣4,2).
(1)求a的值;
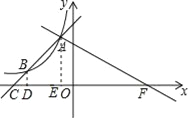
(2)如图,过点B作直线AB与函数y=![]() 的图象交于点A,与x轴交于点C,且AB=3BC,过点A作直线AF⊥AB,交x轴于点F,求线段AF的长.
的图象交于点A,与x轴交于点C,且AB=3BC,过点A作直线AF⊥AB,交x轴于点F,求线段AF的长.

参考答案:
【答案】(1)a=﹣12;(2)AF=8![]() .
.
【解析】试题分析:(1)由反比例函数y=![]() (a为常数)的图象经过点B(﹣4,2),直接利用待定系数法求解即可求得答案;
(a为常数)的图象经过点B(﹣4,2),直接利用待定系数法求解即可求得答案;
(2)首先分别过点A、B作x轴的垂线,垂足分别为点D、E,易得△BCD∽△ACE,即可求得A的坐标,由△ACE∽△FAE,即可求得答案.
试题解析:(1)∵图象过点B(﹣4,2),代入y=![]() ,∴2=
,∴2=![]() ,解得:a=﹣12;
,解得:a=﹣12;
(2)∵a=﹣12,∴反比例函数解析式为![]() ,
,
分别过点A、B作x轴的垂线,垂足分别为点D、E,
∵AB=3BC,∴![]() ,BD=2,
,BD=2,
∵AD∥BE,∴△BCD∽△ACE,∴![]() ,即
,即![]() ,∴AE=8.
,∴AE=8.
∴把y=8代入![]() ,得x=﹣1.∴A(﹣1,8),
,得x=﹣1.∴A(﹣1,8),
设直线AB解析式为y=kx+b,
把A(﹣1,8),B(﹣4,2)代入解析式得, ![]() ,解得:
,解得: ![]() ,
,
∴直线AB解析式为y=2x+10,
当y=0时,2x+10=0,解得:x=﹣5,∴C(﹣5,0),
∴AC=![]() ,
,
∵AF⊥AB,AE⊥CF,∴△ACE∽△FAE,∴![]() ,∴
,∴![]() ,解得:AF=8
,解得:AF=8![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的每一个外角都等于72°,则该多边形的内角和等于________.
-
科目: 来源: 题型:
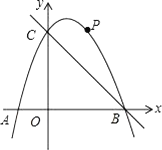
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时点P的坐标和四边形ABPC的最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B、点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN.
(1)当∠BAC=∠MBN=90°时,
①如图a,当θ=45°时,∠ANC的度数为 ;
②如图b,当θ≠45°时,①中的结论是否发生变化?说明理由;
(2)如图c,当∠BAC=∠MBN≠90°时,请直接写出∠ANC与∠BAC之间的数量关系,不必证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=6,求tan∠DEB的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(a2)3=a5
B.a2a=a3
C.a6÷a3=a2
D.(ab)2=ab2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校举办一项小制作评比活动,对初一年级6个班的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1,其中三班的件数是8.

请你回答:
(1)本次活动共有 件作品参赛;
(2)经评比,四班和六班分别有10件和2件作品获奖,那么你认为这两个班中哪个班获奖率较高?为什么?
(3)小制作评比结束后,组委会评出了4件优秀作品A、B、C、D.现决定从这4件作品中随机选出两件进行全校展示,请用树状图或列表法求出刚好展示作品B、D的概率.
相关试题

