【题目】在结束了380课时初中阶段教学内容的教学后,王老师计划按原课程设置再增加70课时用于总复习,将380课时按内容所占比例,绘制如下统计图表(图1、图2),请根据图表提供的信息,回答问题:
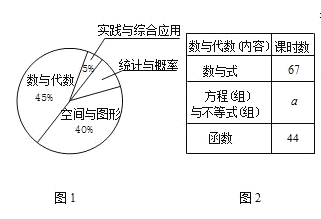
(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2中的a= ;
(3)在70课时的总复习中,王老师应安排多少课时复习图形与几何内容?
参考答案:
【答案】(1)36;(2)60;(3)28
【解析】
(1)用360°乘以“统计与概率”所占的百分比即可;
(2)用总课时数乘以数与代数所占的百分比,再减去数与式和函数的课时数,从而求出a;
(3)用70课时乘以图形与几何所占的百分比即可.
解:(1)图1中“统计与概率”所在扇形的圆心角为:360°×(1﹣45%﹣40%﹣5%)=36(度);
故答案为:36;
(2)图2中的a=380×45%﹣67﹣44=60(节),
故答案为:60;
(3)根据题意得:
70×40%=28(节),
答:王老师应安排28课时复习图形与几何内容.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
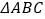 中,
中, 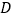 是
是 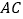 上一点,
上一点, 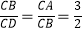 ,
, 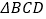 的周长是
的周长是 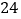 cm.
cm.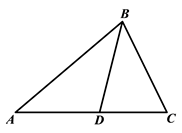
(1)求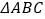 的周长;
的周长;
(2)求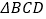 与
与 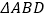 的面积比.
的面积比. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中, BD是∠ABC的平分线,过点C作CE⊥BD,交 BD的延长线于点E,∠ABC=60°,∠ECD=15°.
(1)直接写出∠ADB的度数是_______;
(2)求证:BD=AB;
(3)若AB=2,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P (2a﹣10,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值:
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理;
(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,求△ACE为等腰三角形时CE:CD的值;
(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.
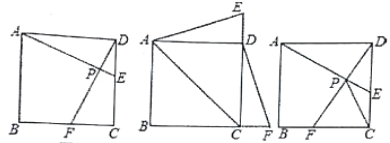
图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能化简(x-1)(x99+x98+x97+…+x+1)吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手,然后归纳出一些方法.
(1)分别化简下列各式:
①(x-1)(x+1)=___________;
②(x-1)(x2+x+1)=___________;
③(x-1)(x3+x2+1)=___________;
……
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=________________.
(2)请你利用上面的结论计算:
299+298+297+…+2+1.
相关试题

