搜索
【题目】如图，在平面直角坐标系中，⊙M与x轴相切于点A（8，0），与y轴分别交于点B（0，4）和点C（0，16），则圆心M到坐标原点O的距离是（ ） 
A.10
B.8 
C.4 
D.2 
参考答案：
【答案】D
【解析】解：如图连接BM、OM，AM，作MH⊥BC于H．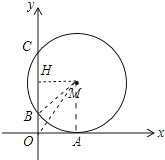
∵⊙M与x轴相切于点A（8，0），
∴AM⊥OA，OA=8，
∴∠OAM=∠MH0=∠HOA=90°，
∴四边形OAMH是矩形，
∴AM=OH，
∵MH⊥BC，
∴HC=HB=6，
∴OH=AM=10，
在RT△AOM中，OM= 
= 
=2 
．
故选D．
如图连接BM、OM，AM，作MH⊥BC于H，先证明四边形OAMH是矩形，根据垂径定理求出HB，在RT△AOM中求出OM即可．本题考查切线的性质、坐标与图形性质、垂径定理、勾股定理等知识，解题的关键是正确添加辅助线，构造直角三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的一元二次方程x2﹣
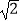x+sinα=0有两个相等的实数根，则锐角α等于（ ）
A.15°
B.30°
C.45°
D.60° -
科目： 来源： 题型：
查看答案和解析>>【题目】某商场销售国外、国内两种品牌的智能手机，这两种手机的进价和售价如表所示
国外品牌
国内品牌
进价（万元/部）
0.44
0.2
售价（万元/部）
0.5
0.25
该商场计划购进两种手机若干部，共需14.8万元，预计全部销售后可获毛利润共2.7万元．[毛利润=（售价﹣进价）×销售量]
（1）该商场计划购进国外品牌、国内品牌两种手机各多少部？
（2）通过市场调研，该商场决定在原计划的基础上，减少国外品牌手机的购进数量，增加国内品牌手机的购进数量．已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍，而且用于购进这两种手机的总资金不超过15.6万元，该商场应该怎样进货，使全部销售后获得的毛利润最大？并求出最大毛利润
-
科目： 来源： 题型：
查看答案和解析>>【题目】木杆AB斜靠在墙壁上，当木杆的上端A沿墙壁NO竖直下滑时，木杆的底端B也随之沿着射线OM方向滑动．下列图中用虚线画出木杆中点P随之下落的路线，其中正确的是（ ）
A.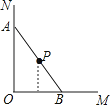
B.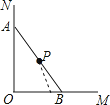
C.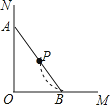
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD是正方形，AC与BD，相交于点O，点E、F是直线AD上两动点，且AE=DF，CF所在直线与对角线BD所在直线交于点G，连接AG，直线AG交BE于点H．
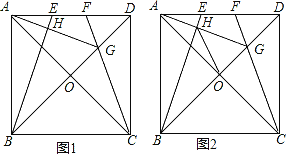
（1）如图1，当点E、F在线段AD上时，求证：∠DAG=∠DCG；
（2）如图1，猜想AG与BE的位置关系，并加以证明；
（3）如图2，在（2）条件下，连接HO，试说明HO平分∠BHG．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠A=30°，BC=2
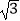，以直角边AC为直径作⊙O交AB于点D，则图中阴影部分的面积是（ ）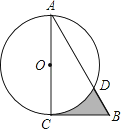 
A.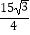
﹣ 
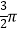
B.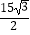
﹣
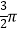
C.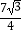
﹣ 
D.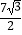
﹣ -
科目： 来源： 题型：
查看答案和解析>>【题目】（题文）图1是一个长为2a，宽为2b的长方形，沿图中虚线剪开分成四块小长方形，然后按图2的形状拼成一个正方形.
图2的阴影部分的正方形的边长是______.
用两种不同的方法求图中阴影部分的面积.（方法1）
= ____________；（方法2）
= ____________；(3) 观察图2，写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系；
根据
题中的等量关系，解决问题：若m+n=10,m-n=6，求mn的值.
相关试题
