【题目】合肥合家福超市为了吸引顾客,设计了一种促销活动:在三等分的转盘上依次标有“合”,“家”,“福”字样,购物每满200元可以转动转盘1次,转盘停下后,指针所指区域是“福”时,便可得到30元购物券(指针落在分界线上不计次数,可重新转动一次),一个顾客刚好消费400元,并参加促销活动,转了2次转盘.
(1)求出该顾客可能获得购物券的最高金额和最低金额;
(2)请用画树状图法或列表法求出该顾客获购物券金额不低于30元的概率.
参考答案:
【答案】(1)最高金额为60元、最低金额为0元;(2)![]()
【解析】
(1)两次都抽到“福”时可得最高金额,两次都没有抽到“福”时可得最低金额;
(2)画出树状图,利用概率公式计算即可;
解:(1)根据题意,该顾客可能获得购物券的最高金额为60元、最低金额为0元;
(2)画树状图如下:
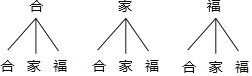
由树状图知,共有9种等可能结果,其中该顾客获购物券金额不低于30元的有5种结果,
所以该顾客获购物券金额不低于30元的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠AOB=70°,以点O为圆心,以适当长为半径作弧分别交OA,OB于C,D两点;分别以C,D为圆心,以大于
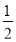 CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____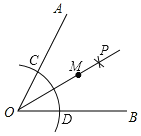
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段
频数
频率
60≤x<70
30
0.15
70≤x<80
m
0.45
80≤x<90
60
n
90≤x≤100
20
0.1
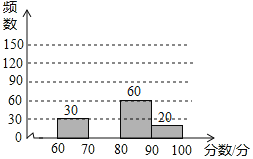
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
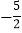
﹣4
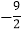
﹣4
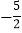
0

…
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界500强H公司决定购买某演唱会门票奖励部分优秀员工,演唱会的购票方式有以下两种,
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元(其中总费用=广告赞助费+门票费);
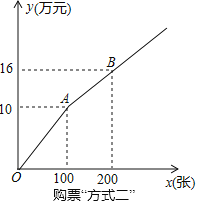
方式二:如图所示,设购买门票x张,总费用为y万元
(1)求用购票“方式一”时y与x的函数关系式;
(2)若H、A两家公司分别釆用方式一、方式二购买本场演唱会门票共400张,且A公司购买超过100张,两公司共花费27.2万元,求H、A两公司各购买门票多少张?
-
科目: 来源: 题型:
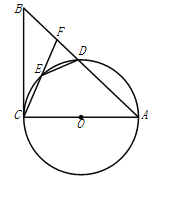
查看答案和解析>>【题目】如图,在⊿
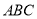 中,以
中,以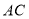 为直径的⊙
为直径的⊙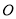 与边
与边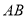 交于点
交于点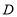 ,点
,点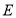 为⊙
为⊙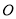 上一点,连接
上一点,连接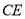 并延长交
并延长交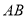 于点
于点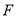 ,连接
,连接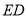 .
.
(1)若
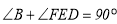 ;求证:
;求证: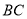 是⊙
是⊙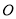 的切线;
的切线;(2)若
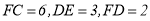 .求⊙
.求⊙ 的直径.
的直径.
相关试题

