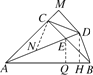
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE交AE延长线于D,DM⊥AC交AC的延长线于M,连接CD,以下四个结论:

①∠ADC=45°;②BD=![]() AE;③AC+CE=AB;④AC+AB=2AM.其中正确的结论有( )
AE;③AC+CE=AB;④AC+AB=2AM.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】
①过E作EQ⊥AB于Q.根据角平分线定义和勾股定理及等腰直角三角形性质得AB=AQ+BQ=AC+CE.②作∠ACN=∠BCD,交AD于N.证△ACN≌△BCD(ASA),得CN=CD.根据等腰直角三角形性质得AN=CN,∠NCE=∠AEC=67.5°,CN=NE,CD=AN=EN=![]() AE;③过D作DH⊥AB于H,根据等腰三角形性质和角平分线定义,△DCM≌△DBH(AAS),BH=CM.由勾股定理得AM=AH,所以AC+AB=AC+AH+BH=AC+AM+CM=2AM.
AE;③过D作DH⊥AB于H,根据等腰三角形性质和角平分线定义,△DCM≌△DBH(AAS),BH=CM.由勾股定理得AM=AH,所以AC+AB=AC+AH+BH=AC+AM+CM=2AM.
过E作EQ⊥AB于Q.
∵∠ACB=90°,AE平分∠CAB,
∴CE=EQ.
∵∠ACB=90°,AC=BC,
∴∠CBA=∠CAB=45°.
∵EQ⊥AB,
∴∠EQA=∠EQB=90°.
由勾股定理得AC=AQ,
∴∠QEB=45°=∠CBA,
∴EQ=BQ,
∴AB=AQ+BQ=AC+CE,
∴①③正确;
作∠ACN=∠BCD,交AD于N.
∵∠CAD=![]() ∠CAB=22.5°=∠BAD,
∠CAB=22.5°=∠BAD,
∴∠DBA=90°-22.5°=67.5°,
∴∠DBC=67.5°-45°=22.5°,
∴∠DBC=∠CAD.在△ACN和△BCD中,
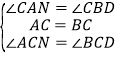
∴△ACN≌△BCD(ASA),CN=CD.
∵∠ACN+∠NCE=90°,
∴∠NCB+∠BCD=90°,
∴∠CND=∠CDN=45°,
∴∠ACN=45°-22.5°=22.5°=∠CAN,
∴AN=CN,
∴∠NCE=∠AEC=67.5°,
∴CN=NE,
∴CD=AN=EN=![]() AE,
AE,
∴②正确;
过D作DH⊥AB于H,
∵∠MCD=∠CAD+∠CDA=67.5°,∠DBA=90°-∠DAB=67.5°,
∴∠MCD=∠DBA.
∵AE平分∠CAB,DM⊥AC,DH⊥AB,
∴DM=DH.在△DCM和△DBH中,
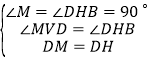
∴△DCM≌△DBH(AAS),
∴BH=CM.
由勾股定理得AM=AH,
∴AC+AB=AC+AH+BH=AC+AM+CM=2AM,
∴④正确.
故选:D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线 ②∠ADC=60°
③点D在AB的垂直平分线上 ④AB=2AC.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程,是一元二次方程的是( )
①3x2+x=20,②2x2﹣3xy+4=0,③x2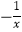 =4,④x2=0,⑤x2﹣3x﹣4=0.
=4,④x2=0,⑤x2﹣3x﹣4=0.
A.①②
B.①②④⑤
C.①③④
D.①④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )

A.4
B.6
C.3
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠ABC=90°,AB=BC,点D是AC的中点,直角∠EDF的两边分别交AB、BC于点E、F,给出以下结论:①AE=BF;②S四边形BEDF=
 S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.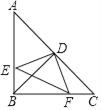
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CA=CB,CD=CE,∠ACB=∠DCE=40°,AD、BE交于点H,连接CH,则∠CHE=__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.

相关试题

