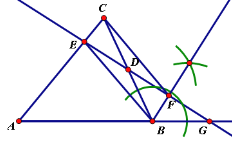
【题目】（8分）如图，△ABC是等腰三角形，AB＝BC，点D为BC的中点．

（1）用圆规和没有刻度的直尺作图，并保留作图痕迹：

①过点B作AC的平行线BP；

②过点D作BP的垂线，分别交AC，BP，BQ于点E，F，G．

（2）在（1）所作的图中，连接BE，CF．求证：四边形BFCE是平行四边形．

参考答案：

【答案】（1）作图见解析；（2）证明见解析．

【解析】

试题（1）①作∠CBQ的平分线BP；②过点D作BP的垂线；

由BP//CE，可得∠ECD=∠FBD，∠CED=∠BFD，又CD=BD，从而△CDE≌△BDF，可得CE=BF，从而可得BF//CE，BF=CE，判定出四边形BFCE是平行四边形．

试题解析：（1）①作∠CBQ的平分线BP；②过点D作BP的垂线；

（2）∵BP//CE，∴∠ECD=∠FBD，∠CED=∠BFD，∵点D是BC的中点，∴CD=BD，∴△CDE≌△BDF，∴CE=BF，∵BF//CE，BF=CE，∴四边形BFCE是平行四边形．

关闭