【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a=﹣![]() .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是3个,请直接写出a的值.

参考答案:
【答案】(1)①D的坐标是(3,1),抛物线的解析式为y=﹣![]() x2+
x2+![]() x;②在抛物线上是否存在点P(
x;②在抛物线上是否存在点P(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),使得∠POB与∠BCD互余;(2)a的值为a=
),使得∠POB与∠BCD互余;(2)a的值为a=![]() .
.
【解析】
试题分析: (1)①过点D作DF⊥x轴于点F,先通过三角形全等求得D的坐标,把D的坐标和a=﹣![]() ,c=0代入y=ax2+bx+c即可求得抛物线的解析式;②先证得CD∥x轴,进而求得要使得∠POB与∠BCD互余,则必须∠POB=∠BAO,设P的坐标为(x,﹣
,c=0代入y=ax2+bx+c即可求得抛物线的解析式;②先证得CD∥x轴,进而求得要使得∠POB与∠BCD互余,则必须∠POB=∠BAO,设P的坐标为(x,﹣ ![]() x2+
x2+![]() x),分两种情况讨论即可求得;(2)若符合条件的Q点的个数是3个,根据tan∠QOB=tan∠BAO=
x),分两种情况讨论即可求得;(2)若符合条件的Q点的个数是3个,根据tan∠QOB=tan∠BAO=![]() =
=![]() ,得到直线OQ的解析式为y=﹣
,得到直线OQ的解析式为y=﹣![]() x,要使直线OQ与抛物线y=ax2+bx+c有一个交点,所以方程ax2﹣4ax+3a+1=﹣
x,要使直线OQ与抛物线y=ax2+bx+c有一个交点,所以方程ax2﹣4ax+3a+1=﹣![]() x有两个相等的实数根,所以△=(﹣4a+
x有两个相等的实数根,所以△=(﹣4a+![]() )2﹣4a(3a+1)=0,即4a2﹣8a+
)2﹣4a(3a+1)=0,即4a2﹣8a+![]() =0,解得a=
=0,解得a=![]() ,根据实际情况对a进行取值即可.
,根据实际情况对a进行取值即可.
试题解析:(1)①过点D作DF⊥x轴于点F,如图1,
∵∠DBF+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠DBF=∠BAO,
又∵∠AOB=∠BFD=90°,AB=BD,
∴△AOB≌△BFD(AAS)
∴DF=BO=1,BF=AO=2,
∴D的坐标是(3,1),
根据题意,得a=﹣![]() ,c=0,且a×32+b×3+c=1,
,c=0,且a×32+b×3+c=1,
∴b=![]() ,
,
∴该抛物线的解析式为y=﹣![]() x2+
x2+![]() x;
x;
②∵点A(0,2),B(1,0),点C为线段AB的中点,
∴C(![]() ,1),
,1),
∵C、D两点的纵坐标都为1,
∴CD∥x轴,
∴∠BCD=∠ABO,
∴∠BAO与∠BCD互余,
要使得∠POB与∠BCD互余,则必须∠POB=∠BAO,
设P的坐标为(x,﹣![]() x2+
x2+![]() x),
x),
(Ⅰ)当P在x轴的上方时,过P作PG⊥x轴于点G,如图2,
则tan∠POB=tan∠BAO,即![]() =
=![]() ,
,
∴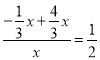 ,解得x1=0(舍去),x2=
,解得x1=0(舍去),x2=![]() ,
,
∴﹣![]() x2+
x2+![]() x=
x=![]() ,
,
∴P点的坐标为(![]() ,
,![]() );
);
(Ⅱ)当P在x轴的下方时,过P作PG⊥x轴于点G,如图3
则tan∠POB=tan∠BAO,即![]() =
=![]() ,
,
∴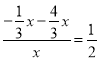 ,解得x1=0(舍去),x2=
,解得x1=0(舍去),x2=![]() ,
,
∴﹣![]() x2+
x2+![]() x=﹣
x=﹣![]() ,
,
∴P点的坐标为(![]() ,﹣
,﹣![]() );
);
综上,在抛物线上是否存在点P(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),使得∠POB与∠BCD互余.
),使得∠POB与∠BCD互余.
(2)如图3,∵D(3,1),E(1,1),
抛物线y=ax2+bx+c过点E、D,代入可得![]() ,解得
,解得![]() ,
,
所以y=ax2﹣4ax+3a+1.
分两种情况:
①当抛物线y=ax2+bx+c开口向下时,若满足∠QOB与∠BCD互余且符合条件的Q点的个数不可能是3个
②当抛物线y=ax2+bx+c开口向上时,
(i)当点Q在x轴的上方时,直线OQ与抛物线y=ax2+bx+c必有两个交点,符合条件的点Q必定有2个;
(ii)当点Q在x轴的下方时,要使直线OQ与抛物线y=ax2+bx+c只有1个交点,才能使符合条件的点Q共3个.
根据(2)可知,要使得∠QOB与∠BCD互余,则必须∠QOB=∠BAO,
∴tan∠QOB=tan∠BAO=![]() =
=![]() ,此时直线OQ的解析式为y=﹣
,此时直线OQ的解析式为y=﹣![]() x,要使直线OQ与抛物线y=ax2+bx+c有一个交点,所以方程ax2﹣4ax+3a+1=﹣
x,要使直线OQ与抛物线y=ax2+bx+c有一个交点,所以方程ax2﹣4ax+3a+1=﹣![]() x有两个相等的实数根,所以△=(﹣4a+
x有两个相等的实数根,所以△=(﹣4a+![]() )2﹣4a(3a+1)=0,即4a2﹣8a+
)2﹣4a(3a+1)=0,即4a2﹣8a+![]() =0,解得a=
=0,解得a=![]() ,
,
∵抛物线的顶点在x轴下方
∴![]() <0,
<0,
∴a>1,
∴a=![]() 舍去
舍去
综上所述,a的值为a=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着以下数字的卡片,请你按要求抽出卡片,完成下列各题.

(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最小,最小值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1﹣(﹣2)]=8×3=24),请另写出一种符合要求的运算式子 . -
科目: 来源: 题型:
查看答案和解析>>【题目】画出数轴,并在数轴上表示下列各数的点2,﹣|﹣3|,﹣1.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
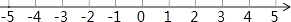
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面由火柴棒拼出的一列图形中,第n个图形由n个正方形组成:
通过观察可以发现:第4个图形中,火柴棒有____根,第n个图形中,火柴棒有_________________根,若用y表示火柴棒的根数,x表示正方形的个数,则y与x的函数关系式是______________________,y是x的____函数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着以下数字的卡片,请你按要求抽出卡片,完成下列各题.
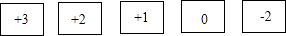
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最小,最小值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1﹣(﹣2)]=8×3=24),请另写出一种符合要求的运算式子 . -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2﹣2y2=_____.
相关试题

