【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.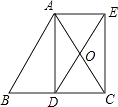
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.
参考答案:
【答案】
(1)证明:∵点O是AC中点,
∴AO=OC,
∵OE=OD,
∴四边形ADCE是平行四边形,
∵AD是等腰△ABC底边BC上的高,
∴∠ADC=90°,
∴四边形ADCE是矩形;
(2)解:∵AD是等腰△ABC底边BC上的高,BC=16,AB=17,
∴BD=CD=8,AB=AC=17,∠ADC=90°,
由勾股定理得:AD= ![]() =
= ![]() =15,
=15,
∴四边形ADCE的面积是AD×DC=15×8=120.
【解析】(1)先证四边形ADCE是平行四边形,再证∠ADC=90°,即可得证;
(2)利用等腰三角形的性质求出CD的长,由勾股定理求出AD的长,再根据矩形的面积公式来求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中∠BAC=135°,点E,点F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,BE=12,CF=9.
(1)判断△EAF的形状,并说明理由;
(2)求△EAF的周长.
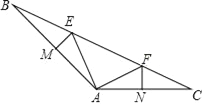
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.
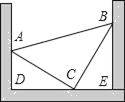
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=
 BC,连接CD和EF.
BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,每个小立方体的棱长为1,图1中共有1个立方体,其中1个看得见,0个看不见;图2中共有8个小立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;……;则第10个图形中,其中看得见的小立方体个数是( )
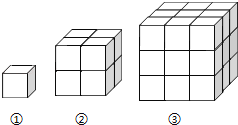
A. 270 B. 271 C. 272 D. 273
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△PQR在直角坐标系中的位置如图所示:
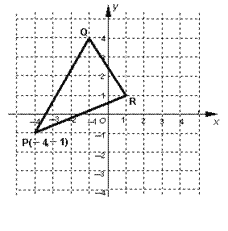
(1) 求出△PQR的面积;
(2) 画出△P′Q′R′,使△P′Q′R′与△PQR关于y轴对称,写出点P′、Q′、R′的坐标;
(3)连接PP′,QQ′,判断四边形QQ′P′P的形状,求出四边形QQ′P′P的面积.
-
科目: 来源: 题型:
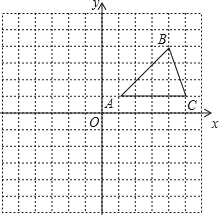
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的位置如图所示,(每个小方格都是边长为1个单位长度的正方形).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转180°,画出旋转后得到的△A2B2C2,并直接写出点B2,C2的坐标.
相关试题

