搜索
【题目】下列说法中，错误的是（ ）
A.在直角三角形ABC中，已知两边长为3和4，则第三边长一定为5；
B.三角形的三边a、b、c满足a2+b2=c2，则∠C=90°；
C.△ABC中，若∠A：∠B：∠C=1：2：3，则△ABC是直角三角形；
D.△ABC中，若a：b：c=3：4：5，则这个三角形是直角三角形．
参考答案：
【答案】A
【解析】
利用分类讨论对①进行判断；根据勾股定理的逆定理对②④进行判断；根据三角形内角和计算出∠C的度数，然后根据三角形分类对③进行判断．
解：在直角三角形ABC中，已知两边长为3和4，则第三边长为5或
，所以A错误；
三角形的三边a、b、c满足
，则
，所以B正确；
△ABC中，若∠A：∠B：∠C=1：2：3，则
，所以△ABC是直角三角形，所以C正确；
△ABC中，若a：b：c=3:4：5，则，所以这个三角形是直角三角形，所以D正确．
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙、丙三位运动员在相同条件下各射靶10次，每次射靶的成绩如下：
甲：9，10，8，5，7，8，10，8，8，7；
乙：5，7，8，7，8，9，7，9，10，10；
丙：7，6，8，5，4，7，6，3，9，5．
（1）根据以上数据求出表中a，b，c的值；
平均数
中位数
方差
甲
8
8
b
乙
a
8
2.2
丙
6
c
3
（2）根据表中数据分析，哪位运动员的成绩最稳定，并简要说明理由；
（3）比赛时三人依次出场，顺序由抽签方式决定，用列举法求甲、乙相邻出场的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在一个坡角为30°的斜坡上有一电线杆AB，当太阳光与水平线成45°角时，测得该杆在斜坡上的影长BC为20m．求电线杆AB的高（精确到0.1m，参考数值：
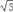≈1.73，
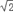≈1.41）．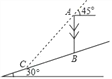
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx（a≠0）过点E（10，0），矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上．设A（t，0），当t=2时，AD=4．
（1）求抛物线的函数表达式．
（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？
（3）保持t=2时的矩形ABCD不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P在⊙O的直径AB的延长线上，PC为⊙O的切线，点C为切点，连接AC，过点A作PC的垂线，点D为垂足，AD交⊙O于点E．
(1)如图1，求证：∠DAC=∠PAC；
(2)如图2，点F（与点C位于直径AB两侧）在⊙O上，
，连接EF，过点F作AD的平行线交PC于点G，求证：FG=DE+DG；(3)在(2)的条件下，如图3，若AE=
DG，PO=5，求EF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知△ABC中，AB=10cm，AC=8cm，BC=6cm．如果点P由B出发沿BA方向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm/s．连接PQ，设运动的时间为t（单位：s）（0≤t≤4）．解答下列问题：
（1）当t为何值时，PQ∥BC．
（2）设△AQP面积为S（单位：cm2），当t为何值时，S取得最大值，并求出最大值．
（3）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在，求出此时t的值；若不存在，请说明理由．
（4）如图2，把△AQP沿AP翻折，得到四边形AQPQ′．那么是否存在某时刻t，使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，剪两张对边平行且宽度相等的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（ ）
A. ∠ABC=∠ADC，∠BAD=∠BCD B. AB=BC
C. AB=CD，AD=BC D. ∠DAB+∠BCD=180°
相关试题
