【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据求出表中a,b,c的值;
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | b |
乙 | a | 8 | 2.2 |
丙 | 6 | c | 3 |
(2)根据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定,用列举法求甲、乙相邻出场的概率.
参考答案:
【答案】(1)a=8,b=2,c=6;(2) 甲的成绩最稳定;(3)![]() .
.
【解析】
(1)根据方差公式和中位数、平均数的定义分别进行解答即可;
(2)根据方差的意义即方差越小越稳定即可得出答案;
(3)根据题意先画出树状图,得出所有情况数和甲、乙相邻出场的情况数,再根据概率公式即可得出答案.
解:(1)乙的平均数a=![]() =8;
=8;
∵甲的平均数是8,
∴甲的方差为b=![]() [(5﹣8)2+2(7﹣8)2+4(8﹣8)2+(9﹣8)2+2(10﹣8)2]=2;
[(5﹣8)2+2(7﹣8)2+4(8﹣8)2+(9﹣8)2+2(10﹣8)2]=2;
把丙运动员的射靶成绩从小到大排列为:3,4,5,5,6,6,7,7,8,9,则中位数c=![]() =6;
=6;
(2)∵甲的方差<乙的方差<丙的方差,而方差越小,数据波动越小,
∴甲的成绩最稳定.
(3)根据题意画图如下:
![]()
∵共有6种情况数,甲、乙相邻出场的有4种情况,
∴甲、乙相邻出场的概率是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为三角形内一点,且△DBC为等边三角形.
(1)求证:直线AD垂直平分BC;
(2)以AB为一边,在AB的右侧画等边△ABE,连接DE,试判断以DA,DB,DE三条线段是否能构成直角三角形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实验与操作:根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF
探究与猜想:若∠BAE=36°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒1cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t(t>0)秒.
(1)AC= cm;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP为等腰三角形(直接写出结果)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:
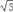 ≈1.73,
≈1.73,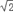 ≈1.41).
≈1.41).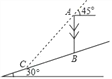
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx(a≠0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.
(1)求抛物线的函数表达式.
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,错误的是( )
A.在直角三角形ABC中,已知两边长为3和4,则第三边长一定为5;
B.三角形的三边a、b、c满足a2+b2=c2,则∠C=90°;
C.△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形;
D.△ABC中,若a:b:c=3:4:5,则这个三角形是直角三角形.
相关试题

