【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与点B,C重合),过点C作CN⊥DM交AB于点N,连结OM、ON,MN.下列五个结论:①△CNB≌△DMC;②ON=OM;③ON⊥OM;④若AB=2,则S△OMN的最小值是1;⑤AN2+CM2=MN2.其中正确结论是_____;(只填序号)

参考答案:
【答案】①②③⑤
【解析】
①由正方形的性质得出CD=BC,∠BCD=90°,证出∠BCN=∠CDM,由ASA即可得出结论;
②由全等三角形的性质得出CM=BN,由正方形的性质得出∠OCM=∠OBN=45°,OC=OB,由SAS证得△OCM≌△OBN(SAS)即可得出结论;
③由△OCM≌△OBN,得出∠COM=∠BON,则∠BOM+∠COM=∠BOM+∠BON,即可得出结论;
④由AB=2,得出S正方形ABCD=4,由△OCM≌△OBN得出四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1,推出△MNB的面积有最大值![]() 即可得出结论;
即可得出结论;
⑤由CM=BN,BM=AN,由勾股定理即可得出结论.
①∵正方形ABCD中,CD=BC,∠BCD=90°,
∴∠BCN+∠DCN=90°,
∵CN⊥DM,
∴∠CDM+∠DCN=90°,
∴∠BCN=∠CDM,
在△CNB和△DMC中
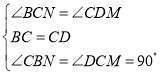 ,
,
∴△CNB≌△DMC(ASA),
故①正确;
②∵△CNB≌△DMC,
∴CM=BN,
∵四边形ABCD是正方形,
∴∠OCM=∠OBN=45°,OC=OB,
在△OCM和△OBN中,
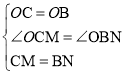 ,
,
∴△OCM≌△OBN(SAS),
∴OM=ON,
故②正确;
③∵△OCM≌△OBN,
∴∠COM=∠BON,
∴∠BOM+∠COM=∠BOM+∠BON,即∠NOM=∠BOC=90°,
∴ON⊥OM;
故③正确;
④∵AB=2,
∴S正方形ABCD=4,
∵△OCM≌△OBN,
∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1,
∴当△MNB的面积最大时,△MNO的面积最小,
设BN=x=CM,则BM=2﹣x,
∴△MNB的面积S=![]() x(2﹣x)=﹣
x(2﹣x)=﹣![]() x2+x=﹣
x2+x=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴当x=1时,△MNB的面积有最大值![]() ,
,
此时S△OMN的最小值是1﹣![]() =
=![]() ,
,
故④不正确;
⑤∵AB=BC,CM=BN,
∴BM=AN,
在Rt△BMN中,BM2+BN2=MN2,
∴AN2+CM2=MN2,
故⑤正确;
∴本题正确的结论有:①②③⑤,
故答案为①②③⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中装有大小相同的2个红球和2个绿球.
(1)先从袋中摸出1个球后放回,混合均匀后再摸出1个球.
①求第一次摸到绿球,第二次摸到红球的概率;
②求两次摸到的球中有1个绿球和1个红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校艺术节要印制节目单,有两个印刷厂前来联系业务,他们的报价相同,甲厂的优惠条件是:按每份定价1.5元的八折收费,另收900元制版费;乙厂的优惠条件是:每份定价1.5元的价格不变,而900元的制版费则六折优惠.问:
(1)学校印制多少份节目单时两个印刷厂费用是相同的?
(2)学校要印制1500份节目单,选哪个印刷厂所付费用少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.
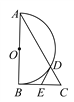
(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
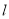 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥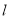 于点D.
于点D.(1)如图①,当直线
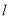 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;(2)如图②,当直线
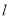 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.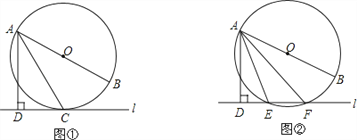
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD,且BC=6时,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的集合内:+8.5,-3
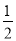 ,0.3,0,-3.4,12,-9,4
,0.3,0,-3.4,12,-9,4 ,-1.2,-2.
,-1.2,-2.(1)正数集合:{___________…};
(2)整数集合:{___________…};
(3)非正整数集合:{_____________…};
(4)负分数集合:{ ________________…}.
相关试题

