【题目】如图,矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD,且BC=6时,求CD的长.

参考答案:
【答案】(1)详见解析;(2)3
【解析】
(1)因为BF![]() CD,已经有一组对边平行我们想到可以运用一组对边平行且相等这个判定定理来证明,所以只需要证明AF=CD就可以通过证明四边形AFDC是平行四边形.
CD,已经有一组对边平行我们想到可以运用一组对边平行且相等这个判定定理来证明,所以只需要证明AF=CD就可以通过证明四边形AFDC是平行四边形.
(2)因为AE=ED,![]() ,且CF平分
,且CF平分![]() ,所以
,所以![]() 是等腰三角形,即ED=DC
是等腰三角形,即ED=DC
证明:(1)∵四边形ABCD是矩形,
∴AB∥CD,AD=BC,
∴∠FAE=∠CDE.
∵E是AD的中点,
∴AE=DE.
在△FAE和△CDE中, ,
,
∴△FAE≌△CDE(AAS),
∴CD=FA.
又∵CD∥AF,
∴四边形ACDF是平行四边形;
(2)解:∵CF平分∠BCD,
∴∠DCE=45°.
∵∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CD=DE.
∵E是AD的中点,
∴CD=![]() AD=
AD=![]() BC=3.
BC=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.
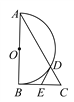
(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与点B,C重合),过点C作CN⊥DM交AB于点N,连结OM、ON,MN.下列五个结论:①△CNB≌△DMC;②ON=OM;③ON⊥OM;④若AB=2,则S△OMN的最小值是1;⑤AN2+CM2=MN2.其中正确结论是_____;(只填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
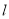 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥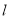 于点D.
于点D.(1)如图①,当直线
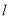 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;(2)如图②,当直线
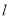 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.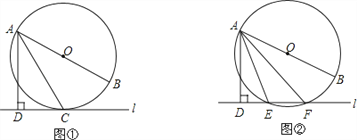
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的集合内:+8.5,-3
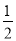 ,0.3,0,-3.4,12,-9,4
,0.3,0,-3.4,12,-9,4 ,-1.2,-2.
,-1.2,-2.(1)正数集合:{___________…};
(2)整数集合:{___________…};
(3)非正整数集合:{_____________…};
(4)负分数集合:{ ________________…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作
y轴的平行线,与直线AC交于点G(点G在点F的上方).若,
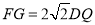
求点F的坐标.

-
科目: 来源: 题型:
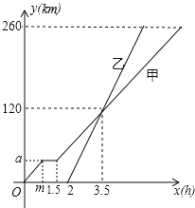
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)直接写出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x (h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车出发多长时间后,两车恰好相距40km?
相关试题

