【题目】下列各数填在相应的集合内,注意数与数要用逗号隔开
![]() ,
,![]() ,0 ,
,0 ,![]() ,8 ,-2 ,25% ,-3.8 ,0.1011 ,100 ,-200
,8 ,-2 ,25% ,-3.8 ,0.1011 ,100 ,-200
负数集合:{ …};
整数集合:{ … };
非负集合:{ … };
分数集合:{ … };
参考答案:
【答案】![]() ,
, ![]() , -2 ,-3.8, -200;0, 8, -2, 100, -200;
, -2 ,-3.8, -200;0, 8, -2, 100, -200;![]() , 0, 8, 25%, 0.1011, 100;
, 0, 8, 25%, 0.1011, 100;![]() ,
, ![]() ,
, ![]() , 25%, -3.8, 0.1011.
, 25%, -3.8, 0.1011.
负数集合:{ ![]() ,
, ![]() , -2 ,-3.8,-200 …};
, -2 ,-3.8,-200 …};
整数集合:{0, 8, -2, 100, -200 … };
非负集合:{![]() , 0, 8, 25%, 0.1011, 100 … };
, 0, 8, 25%, 0.1011, 100 … };
分数集合:{![]() ,
, ![]() ,
, ![]() , 25%,-3.8, 0.1011, … };
, 25%,-3.8, 0.1011, … };
【解析】
利用负数,整数,分数,以及非负数定义判断即可.
负数:比0小的数叫负数;
非负数:正数和零的总称.;
分数:分数是一个整数a和一个正整数b的不等于整数的比.
负数集合:{ ![]() ,
, ![]() , -2 ,-3.8,-200 …};
, -2 ,-3.8,-200 …};
整数集合:{0, 8, -2, 100, -200 … };
非负集合:{![]() , 0, 8, 25%, 0.1011, 100 … };
, 0, 8, 25%, 0.1011, 100 … };
分数集合:{![]() ,
, ![]() ,
, ![]() , 25%,-3.8, 0.1011, … };
, 25%,-3.8, 0.1011, … };
-
科目: 来源: 题型:
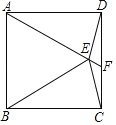
查看答案和解析>>【题目】如图,在正方形ABCD中,△ABE为等边三角形,连接DE,CE,延长AE交CD于F点,则∠DEF的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解方程:
(1)x2﹣4x﹣5=0;
(2)y(y﹣7)=14﹣2y;
(3)2x2﹣3x﹣1=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位自然数是
 ,将它任意两个数位的数字对调后得到一个首位不为0的新三位自然数
,将它任意两个数位的数字对调后得到一个首位不为0的新三位自然数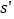 (
(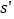 可以与
可以与 相同),设
相同),设 ,在
,在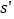 所有的可能情况中,当
所有的可能情况中,当 最大时,我们称此时的
最大时,我们称此时的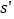 是
是 的“梦想数”,并规定
的“梦想数”,并规定 .例如127按上述方法可得到新数有:217、172、721,因为
.例如127按上述方法可得到新数有:217、172、721,因为 所以172是172的“梦想数”,此时,
所以172是172的“梦想数”,此时, .
.(1)求512的“梦想数”及
 的值;
的值;(2)设三位自然数
 交换其个位与十位上的数字得到新数
交换其个位与十位上的数字得到新数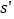 ,若
,若 ,且
,且 能被7整除,求
能被7整除,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 与
与 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与 轴交于点C,顶点为D,对称轴与
轴交于点C,顶点为D,对称轴与 轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交
轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交 轴交于点G.
轴交于点G.(1)如图①,求直线CE的解析式和顶点D的坐标;
(2)如图①,点P为直线CF上方抛物线上一点,连接PC、PF,当△PCF的面积最大时,点M是过P垂直于
 轴的直线l上一点,点N是抛物线对称轴上一点,求
轴的直线l上一点,点N是抛物线对称轴上一点,求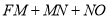 的最小值;
的最小值;(3)如图②,过点D作
 交
交 轴于点I,将△GDI沿射线GB方向平移至
轴于点I,将△GDI沿射线GB方向平移至 处,将
处,将 绕点
绕点 逆时针旋转
逆时针旋转 ,当旋转到一定度数时,点
,当旋转到一定度数时,点 会与点I重合,记旋转过程中的
会与点I重合,记旋转过程中的 为
为 ,若在整个旋转过程中,直线G’’I’’分别交x轴和直线GD’于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.
,若在整个旋转过程中,直线G’’I’’分别交x轴和直线GD’于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):
 .问:
.问:(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
-
科目: 来源: 题型:
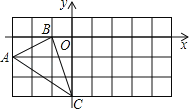
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,﹣1)、B(﹣1,0)、C(0,﹣3)
(1)点A关于坐标原点O对称的点的坐标为 .
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C,A1A的长为 .
相关试题

