【题目】如图,已知正方形ABCD的边长是5,点E在DC上,将△ADE经顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转角度;
(2)如果连接EF,那么△AEF是怎样的三角形?请说明理由;
(3)△ABF向右平移后与△DCH位置,平移的距离是多少?
(4)试猜想线段AE和DH的数量关系和位置关系,并说明理由.
参考答案:
【答案】(1)旋转的中心是点A,旋转的角度是90°;(2)△AEF是等腰直角三角形(3)△ABF向右平移后与△DCH位置,平移的距离是5;(4)AE=DH,AE⊥DH,
【解析】(1)旋转的中心是点A,旋转的角度是90°;
(2)△AEF是等腰直角三角形.
理由如下:
∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴△AEF是等腰直角三角形.
(3)∵正方形ABCD的边长是5,
∴△ABF向右平移后与△DCH位置,平移的距离是5;
(4)AE=DH,AE⊥DH,
理由:∵△ABF向右平移后与△DCH重合,
∴DH∥AF,DH=AF,
又∵△ADE绕着点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴AE⊥AF,
∴AE=DH,AE⊥DH.
【试题分析】(1)根据旋转的定义,直接得出旋转的中心和旋转的角度;
(2)由(1)得到△ADE绕着点A逆时针旋转90°后与△ABF重合,根据旋转的性质得
∠FAE=90°,AF=AE,由此可判断△AEF是等腰直角三角形;
(3)利用旋转中心为正方形对角线的交点,逆时针旋转90°(或逆时针旋转270°),即可得出平移距离等于正方形边长;
(4)根据平移的性质得AF∥DH,由(2)得AF⊥AE,所以AE⊥DH,进而得出AE=DH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若某次数学考试标准成绩定为85分,规定高于标准记为正,两位学生的成绩分别记作:+9分和-3分,则第一位学生的实际得分为___________分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x
···
1
2
3
5
7
9
···
y
···
1.98
3.95
2.63
1.58
1.13
0.88
···
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系
 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=90°.
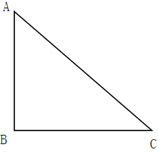
(1)请在BC上找一点P,作⊙P与AC,AB都相切,切点为Q;(尺规作图,保留作图痕迹)
(2)若AB=3,BC=4,求第(1)题中所作圆的半径;
(3)连结BQ,第(2)中的条件均不变,求sin∠CBQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB的长为20,点D在AB上,△ACD是边长为8的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )

A. 10 B. 6 C. 8
 D. 6
D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( ) .
A. 对角线相等的四边形是矩形;
B. 对角线互相垂直的四边形是菱形;
C. 对角线互相平分的四边形是平行四边形;
D. 对角线互相垂直平分的四边形是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是△ABC的边AB上一点,E是AC的中点,过点C作CF//AB,交DE的延长线于点F.
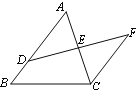
求证:AB=CF+BD.
相关试题

