【题目】如图,在等边![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,
, ![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证: ![]() ;
;
(2)求![]() 的度数.
的度数.
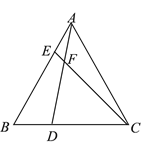
参考答案:
【答案】(1)证明见解析;(2)60°.
【解析】试题分析:(1)根据等边三角形的性质,利用SAS证得△AEC≌△BDA,所以AD=CE;
(2)由(1)△AEC≌△BDA可得∠ACE=∠BAD,再根据三角形的外角与内角的关系得到∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°.
试题解析:(1)∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS),
∴AD=CE;
(2)∵△AEC≌△BDA,
∴∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的面积为49cm2,AE=ED,BD=3DC,则图中△AEF的面积等于___________.
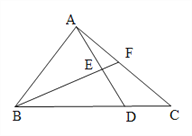
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=120°,DE垂直平分AC,交BC于D,交AC于E,且DE=2cm,求BC的长.
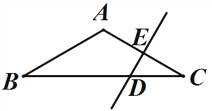
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
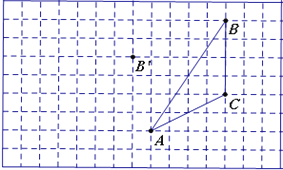
(1) 补全△A′B′C′;
(2) 根据下列条件,利用网格点和直尺画图:
画出△ABC中:
①AC边上的中线BD;
②AC边上的高线BE;
(3)写出△ABD的面积 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知抛物线C:y=x2-4x+4和直线l:y=kx-2k(k>0).
(1)抛物线C的顶点D的坐标为 ;
(2)请判断点D是否在直线
 上,并说明理由;
上,并说明理由;(3)记函数
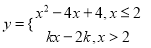 的图像为G,点M(0,t),过点M垂直于
的图像为G,点M(0,t),过点M垂直于 轴的直线与图像G交于点
轴的直线与图像G交于点 .当1<t<3时,若存在t使得
.当1<t<3时,若存在t使得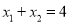 成立,结合图像,求k的取值范围.
成立,结合图像,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,已知∠A=105°,∠B-∠C=15°,求∠C的度数.
相关试题

