【题目】解决下列各小题(第①题4分,每②题5分,第③题6分,满分15分)
①因式分解: ![]() .
.
②解不等式组: 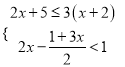 ,并指出它的所有非负整数解.
,并指出它的所有非负整数解.
③化简: ![]() ,再从
,再从![]() ,
, ![]() ,
, ![]() ,
, ![]() 中选一个合适的数代入求值.
中选一个合适的数代入求值.
参考答案:
【答案】(1)![]() ; (2)
; (2)![]() ,
, ![]() ,
, ![]() ; (3)
; (3)![]() ;当
;当![]() 时,原式
时,原式![]()
【解析】试题分析:(1)先利用完全平方公式,单项式乘多项式进行计算,合并同类项后再利用平方差公式进行因式分解即可;
(2)先求出每一个不等式的解集,然后确定不等式组的解集,指出非负整数解即可;
(3)括号内先通分,进行加减运算,然后再进行乘除运算,最后代入数值进行计算即可.
试题解析:(![]() )
)![]() ;
;
(![]() )
)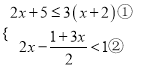 ,
,
由①得: ![]() ,由②得:
,由②得: ![]() ,
,
所以不等式组的解集为![]() ,
,
所以在此范围内的非负整数解有![]() ,
, ![]() ,
, ![]() ;
;
(![]() )原式
)原式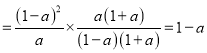 ,
,
因为![]() 且
且![]() ,所以,当
,所以,当![]() 时,原式
时,原式![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若82a+3×8b-2=810,求2a+b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x-2y=3,则代数式6-2x+4y的值为( )
A.0
B.-1
C.-3
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:AE=BE;
(2)求证:FE是⊙O的切线;
(3)若FE=4,FC=2,求⊙O的半径及CG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂期买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金.应该选择哪种方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2
 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DG⊥BE,请你帮他说明理由.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
(3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a3m=3,b3n=2,求(a2m)3+(bn)3-a2m·bn·a4m·b2n的值.
相关试题

