【题目】如下图。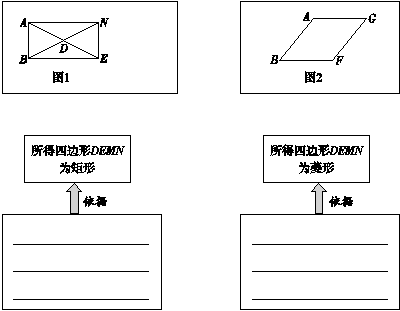
(1)画图-连线-写依据:
先分别完成以下画图(不要求尺规作图),再与判断四边形DEMN形状的相应结论连线,并写出判定依据(只将最后一步判定特殊平行四边形的依据填在横线上).
①如图1,在矩形ABEN中,D为对角线的交点,过点N画直线NP∥DE , 过点E画直线EQ∥DN , NP与EQ的交点为点M , 得到四边形DEMN;
②如图2,在菱形ABFG中,顺次连接四边AB , BF , FG , GA的中点D , E , M , N , 得到四边形DEMN.
(2)请从图1、图2的结论中选择一个进行证明.
参考答案:
【答案】
(1)
解:见图3,图4,连线、
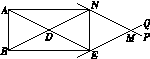
图3依据:有一组邻边相等的平行四边形为菱形.
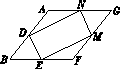
图4依据:有一个角为直角的平行四边形为矩形.
(2)
证明:①如图3.
∵ NP∥DE,EQ∥DN,NP与EQ的交点为点M,
∴ 四边形DEMN为平行四边形.
∵ D为矩形ABEN对角线的交点,
∴ AE=BN, ![]() ,
, ![]() .
.
∴ DE= DN.
∴ 平行四边形DEMN是菱形.
②如图5,连接AF,BG,记交点为H.
∵ D,N两点分别为AB,GA边的中点,
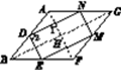
图5
∴ DN∥BG, ![]() .
.
同理,EM∥BG, ![]() ,DE∥AF,
,DE∥AF, ![]() .
.
∴ DN∥EM,DN=EM.
∴ 四边形DEMN为平行四边形.
∵ 四边形ABFG是菱形,
∴ AF⊥BG.
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴ 平行四边形DEMN是矩形
【解析】(1)如图3,依据为有一组邻边相等的平行四边形为菱形.如图4依据为有一个角为直角的平行四边形为矩形.
(2)①如图3.由NP∥DE,EQ∥DN得 四边形DEMN为平行四边形;根据DE= DN得到平行四边形DEMN是菱形.
②如图5,连接AF , BG , 记交点为H.由 D , N、E、M为中点得DN∥EM , DN=EM.所以四边形DEMN为平行四边形.由菱形得![]() =
=![]()
![]()
所以 平行四边形DEMN是矩形。
-
科目: 来源: 题型:
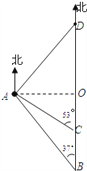
查看答案和解析>>【题目】如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
(参考数据:sin53°≈
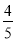 ,cos53°≈
,cos53°≈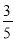 ,tan53°≈
,tan53°≈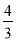 )
) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x2+x2=x4
B.x2+x3=2x5
C.3x﹣2x=1
D.x2y﹣2x2y=﹣x2y -
科目: 来源: 题型:
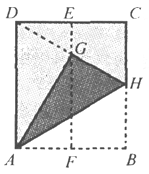
查看答案和解析>>【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )
A. 2cm B.
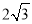 cm C. 4cm D.
cm C. 4cm D. 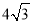 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=
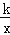 (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( )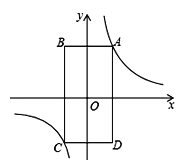
A. 一直增大 B. 一直减小 C. 先增大后减小 D. 先减小后增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下:
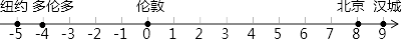
如果将两地国际标准时间的差简称为时差,那么下列说法中正确的是( )
A. 汉城与纽约的时差为13小时 B. 北京与纽约的时差为13小时
C. 北京与纽约的时差为14小时 D. 北京与多伦多的时差为14小时
-
科目: 来源: 题型:
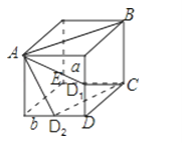
查看答案和解析>>【题目】如图,
(1)一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?
(2)如果要爬行到顶点C呢?说出你的理由.
相关试题

