【题目】如图,矩形![]() 在平面直角坐标系中,
在平面直角坐标系中, ![]() ,
,![]() ,把矩形
,把矩形![]() 沿直线
沿直线![]() 对折使点
对折使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在坐标平面内,若四边形
在坐标平面内,若四边形![]() 是菱形,则菱形
是菱形,则菱形![]() 的面积是( )
的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
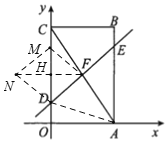
如图,连接AD,根据勾股定理先求出OC的长,然后根据折叠的性质以及勾股定理求出AD、DF的长,继而作出符合题意的菱形,分别求出菱形的两条对角线长,然后根据菱形的面积等于对角线积的一半进行求解即可.
如图,连接AD,
∵∠AOC=90°,AC=5,AO=3,
∴CO=![]() =4,
=4,
∵把矩形![]() 沿直线
沿直线![]() 对折使点
对折使点![]() 落在点
落在点![]() 处,
处,
∴∠AFD=90°,AD=CD,CF=AF=![]() ,
,
设AD=CD=m,则OD=4-m,
在Rt△AOD中,AD2=AO2+OD2,
∴m2=32+(4-m)2,
∴m=![]() ,
,
即AD=![]() ,
,
∴DF=![]() =
=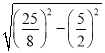 =
=![]() ,
,
如图,过点F作FH⊥OC,垂足为H,延长FH至点N,使HN=HF,在HC上截取HM=HD,则四边形MFDN即为符合条件的菱形,
由题意可知FH=![]() ,
,
∴FN=2FH=3,DH=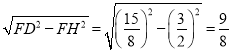 ,
,
∴DM=2DH=![]() ,
,
∴S菱形MFDN=![]() ,
,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AC,点D为AC的中点,B是直线AC上的一点,且 BC
 AB,BD=1,则AC=_____.
AB,BD=1,则AC=_____. -
科目: 来源: 题型:
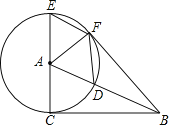
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF,DF.
(1)试探究BF与AF位置关系,并说明理由;
(2)当∠CAB等于多少度时,四边形ADEF为菱形?请给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
 与矩形
与矩形 如图放置,点
如图放置,点 共线,
共线, 共线,连接
共线,连接 ,取
,取 的中点
的中点 ,连接
,连接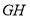 ,若
,若 ,
, ,则
,则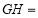 ( )
( )
A.
 B.
B.  C. 2D.
C. 2D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)23×(-5)-(-3)÷
 ;
; (2)(-3)×
 +8×(-2
+8×(-2 )-11÷(-
)-11÷(- );
);(3)(-1)2-(-1
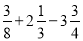 )×(-24);
)×(-24); (4)
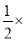 (-2)2-(
(-2)2-(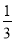 )3+[1+(-
)3+[1+(- )2×(-1
)2×(-1 )].
)]. -
科目: 来源: 题型:
查看答案和解析>>【题目】【阅读学习】 刘老师提出这样一个问题:已知α为锐角,且tanα=
 ,求sin2α的值.
,求sin2α的值.小娟是这样解决的:
如图1,在⊙O中,AB是直径,点C在⊙O上,∠BAC=α,所以∠ACB=90°,tanα=
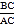 =
= .
.易得∠BOC=2α.设BC=x,则AC=3x,则AB=
 x.作CD⊥AB于D,求出CD= (用含x的式子表示),可求得sin2α=
x.作CD⊥AB于D,求出CD= (用含x的式子表示),可求得sin2α= = .
= .【问题解决】
已知,如图2,点M、N、P为圆O上的三点,且∠P=β,tanβ =
 ,求sin2β的值.
,求sin2β的值.

-
科目: 来源: 题型:
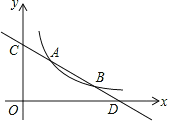
查看答案和解析>>【题目】直线y=kx+b与反比例函数y=
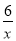 (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
相关试题

