Question

【题目】如图,在ABCD中,E,F是对角线BD上的两点,若添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.BE=DF
B.BF=DE
C.AE=CF
D.∠1=∠2

Answer 1

【答案】C
【解析】∵ABCD
∴AB∥CD，AB=CD
∴∠ABE=∠FDC
A、在△ABE和△CDF中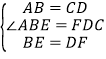

∴△ABE≌△CDF（SAS），因此A不符合题意；
B、∵BF=DE
∴BF-EF=DE-EF，即BE=DF
同A可证明△ABE≌△CDF（SAS），因此B不符合题意；
C、AE=CF，AB=CD，∠ABE=∠FDC，边边角不能证明△ABE≌△CDF，因此C不符合题意；
D、在△ABE和△CDF中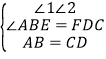

∴△ABE≌△CDF（SAS），因此D不符合题意；
【考点精析】认真审题，首先需要了解平行线的性质(两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补)，还要掌握平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)的相关知识才是答题的关键．