【题目】解下列不等式(组),并把解集在数轴上表示出来.
(1)![]() ≤5﹣x
≤5﹣x
(2)![]() .
.
参考答案:
【答案】
(1)解: ![]() ≤5﹣x
≤5﹣x
x﹣1≤15﹣3x,
x+3x≤15+1,
4x≤16,
解得x≤4,
在数轴上表示不等式的解集为:
![]()
(2)解: 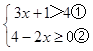
由①得,x>1;
由②得,x≤2;
所以不等式的解集为1<x≤2,
在数轴上表示为:
![]()
【解析】(1)去分母,去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可.(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
【考点精析】通过灵活运用不等式的解集在数轴上的表示和一元一次不等式的解法,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据给出的数轴及已知条件,解答下面的问题:

(1)已知点A,B,C表示的数分别为1,﹣ ,﹣3观察数轴,与点A的距离为3的点表示的数是 , B,C两点之间的距离为;
,﹣3观察数轴,与点A的距离为3的点表示的数是 , B,C两点之间的距离为;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是;若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M , N;
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P , Q(用含m,n的式子表示这两个数). -
科目: 来源: 题型:
查看答案和解析>>【题目】为了考察某区3500名毕业生的数学成绩,从中抽出20本试卷,每本30份,在这个问题中,样本容量是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式一定成立的是( )
A.﹣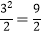
B.|﹣a|=a
C.(﹣a)3=a3
D.(﹣a)2=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=-5x+3的图象经过的象限是( )
A. 一、二、三 B. 二、三、四 C. 一、二、四 D. 一、三、四
-
科目: 来源: 题型:
查看答案和解析>>【题目】要使方程(a﹣3)x2+(b+1)x+c=0是关于x的一元二次方程,则( )
A.a≠0
B.a≠3
C.a≠1且b≠﹣1
D.a≠3且b≠﹣1且c≠0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△abc的三个顶点的坐标分别为A(﹣6,4),B(﹣4,0),C(﹣2,2).
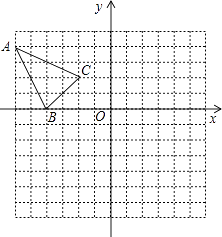
(1)将△ABC向右平移5个单位得,得△A1B1C1 , 画出图形,并直接写出点A1的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,得△A2B2C2 , 画出图形,并直接写出点B2的坐标.
相关试题

