【题目】某儿童服装店欲购进A、B两种型号的儿童服装.经调查:B型号童装的进货单价是A型号童装的进货单价的两倍,购进A型号童装60件和B型号童装40件共用去2100元.
(1)、求A、B两种型号童装的进货单价各是多少元?
(2)、若该店每销售1件A型号童装可获利4元,每销售1件B型号童装可获利9元,该店准备用不超过6300元购进A、B两种型号童装共300件,且这两种型号童装全部售出后总获利不低于1795元.问该店应该怎样安排进货,才能使总获利最大?最大总获利为多少元?
参考答案:
【答案】(1)、A:15元;B:30元;(2)、A型号童装180件,B型号童装120件;总获利1800元.
【解析】
试题分析:(1)、首先设A型号的进货单价为x元,则B型号的进货单价为2x元,根据进货总价列出方程进行求解;(2)、设A型号童装a件,则购进B型号童装(300-a)件,根据题意列出不等式组,然后求出取值范围,列出w和a的函数关系式,然后根据函数的性质进行求解.
试题解析:(1)、设A型号的进货单价为x元,则B型号的进货单价为2x元,
根据题意得:60x+40×2x=2100 解得:x=15,则2x=30
答:A、B两种型号童装的进货单价分别是15元、30元.
、设该店购进A型号童装a件,则购进B型号童装(300-a)件,
根据题意得:![]() 解得:180≤a≤181
解得:180≤a≤181
∵总获利w=4a+9(300-a)=-5a+2700
∴w是关于a的一次函数,并且w随a的增大而减小
∴当a=180时,w最大,最大值为:-5×180+2700=1800 此时300-a=120
答:该店应购进A型号童装180件,B型号童装120件,才能使总获利最大,最大总获利为1800元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=90°,点A、B分别在直线OM、ON上,BC是∠ABN的平分线.
(1)如图1,若BC所在直线交∠OAB的平分线于点D时,尝试完成①、②两题:
①当∠ABO=30°时,∠ADB= °
②当点A、B分别在射线OM、ON上运动时(不与点O重合),试问:随着点A、B的运动,∠ADB的大小会变吗?如果不会,请求出∠ADB的度数;如果会,请求出∠ADB的度数的变化范围;
(2)如图2, 若BC所在直线交∠BAM的平分线于点C时,将△ABC沿EF折叠,使点C落在四边形ABEF内点C′的位置.求∠BEC′+∠AFC′ 的度数.
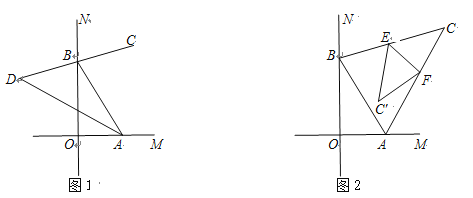
-
科目: 来源: 题型:
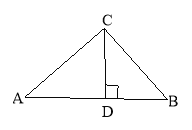
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB于点D,AC=4,BC=3,DB=
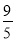 ,
,(1)求CD、AD的长
(2)判断△ABC的形状,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD.
(1)求证:四边形ADCE是矩形;
(2)当∠BAC=90°时,求证:四边形ADCE是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某店出售甲、乙、丙三种不同型号的电动车,已知甲型车的第一季度销售额占这三种车总销售额的56%,第二季度乙、丙两种型号车的销售额比第一季度减少了a%,但该商场电动车的总销售额比第一季度增加了12%,且甲型车的销售额比第一季度增加了23%,则a的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(-2,3)关于原点的对称点Q的坐标为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列两点都在一次函数y=-2x+3的图象上的是( )
A. 原点和点(1,1)B. (1,1)和(2,3)
C. (0,3)和(1,1)D. (0,3)和(2,3)
相关试题

