【题目】如图,∠MON=90°,点A、B分别在直线OM、ON上,BC是∠ABN的平分线.
(1)如图1,若BC所在直线交∠OAB的平分线于点D时,尝试完成①、②两题:
①当∠ABO=30°时,∠ADB= °
②当点A、B分别在射线OM、ON上运动时(不与点O重合),试问:随着点A、B的运动,∠ADB的大小会变吗?如果不会,请求出∠ADB的度数;如果会,请求出∠ADB的度数的变化范围;
(2)如图2, 若BC所在直线交∠BAM的平分线于点C时,将△ABC沿EF折叠,使点C落在四边形ABEF内点C′的位置.求∠BEC′+∠AFC′ 的度数.
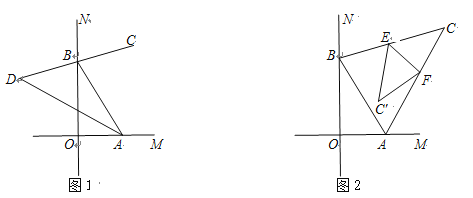
参考答案:
【答案】(1)①45;②∠ADB的大小不会变,为45°;
(2)∠BEC′+∠AFC′ 的度数是90°;
【解析】试题分析: (1) ①根据角平分线的定义可得: ∠NBC=∠ABC,然后根据对顶角相等可得: ∠NBC=∠DBO,然后由已知可得: ∠ABO=30°,然后由三角形外角的性质可得: ∠NBA=∠BOA+∠BAO =120°,进而可得: ∠NBC=∠ABC=60°,然后由AD是∠OAB的平分线得到∠BAD=![]() ∠BAO=15°,最后由∠BAD+∠BDA=∠ABC即可求出答案;
∠BAO=15°,最后由∠BAD+∠BDA=∠ABC即可求出答案;
②∠ADB的大小不随点A,B的移动而发生变化,根据三角形的一个外角等于和它不相邻的两个内角的和, ∠ABN=∠OAB+∠MON, ∠CBA=∠ADB+∠DAB,再根据角平分线的定义∠DAB=![]() ∠OAB, ∠CBA=
∠OAB, ∠CBA=![]() ∠ABN,代入整理即可得到∠ADB=
∠ABN,代入整理即可得到∠ADB=![]() ∠MON=45°.
∠MON=45°.
(2)首先根据已知证出∠C=45°,从而得到∠C EC′+∠CFC′=2(180°-∠C)=270°,进而得到∠BEC′+∠AFC′=360°-(∠C EC′+∠CFC′)=90°。
试题解析:
(1)①45
②设∠ABO=α,
∵∠MON=90°
∴∠BAD=![]() ,∠ABC=
,∠ABC=![]()
∴∠ABD=180°-∠ABC=![]()
∴∠ADB=180°-∠BAD -∠ABD=45°
(2)∵∠MON=90°
∴∠ABO+∠BAO=90°
∴∠CAB+∠CBA=![]() (∠BAM+∠ABN)=135°
(∠BAM+∠ABN)=135°
∴∠C=45°
∴∠C EC′+∠CFC′=2(180°-∠C)=270°
∴∠BEC′+∠AFC′=360°-(∠C EC′+∠CFC′)=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D落到D’处,折痕为EF.
(1)、求证:△ABE≌△AD’F;
(2)、连接CF,判断四边形AECF是否为平行四边形?请证明你的结论。
(3)、若AE=5,求四边形AECF的周长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】五边形的外角和等于度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法取近似数, 1.804≈__________(精确到百分位)
-
科目: 来源: 题型:
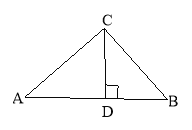
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB于点D,AC=4,BC=3,DB=
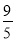 ,
,(1)求CD、AD的长
(2)判断△ABC的形状,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD.
(1)求证:四边形ADCE是矩形;
(2)当∠BAC=90°时,求证:四边形ADCE是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某儿童服装店欲购进A、B两种型号的儿童服装.经调查:B型号童装的进货单价是A型号童装的进货单价的两倍,购进A型号童装60件和B型号童装40件共用去2100元.
(1)、求A、B两种型号童装的进货单价各是多少元?
(2)、若该店每销售1件A型号童装可获利4元,每销售1件B型号童装可获利9元,该店准备用不超过6300元购进A、B两种型号童装共300件,且这两种型号童装全部售出后总获利不低于1795元.问该店应该怎样安排进货,才能使总获利最大?最大总获利为多少元?
相关试题

