【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在
分别在![]() 上(点
上(点![]() 与点
与点![]() 不重合),且
不重合),且![]() .将
.将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() .当
.当![]() 的斜边、直角边与
的斜边、直角边与![]() 分别相交于点
分别相交于点![]() (点
(点![]() 与点
与点![]() 不重合)时,设
不重合)时,设![]() .
.
(1)求证:![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围.
的取值范围.

参考答案:
【答案】(1)见解析;(2)
【解析】
试题分析:(1)根据等角的余角相等即可证明;
(2)分两种情形①如图1中,当C′E′与AB相交于Q时,即![]() 时,过P作MN∥DC′,设∠B=α.②当DC′交AB于Q时,即
时,过P作MN∥DC′,设∠B=α.②当DC′交AB于Q时,即![]() 时,如图2中,作PM⊥AC于M,PN⊥DQ于N,则四边形PMDN是矩形,分别求解即可;
时,如图2中,作PM⊥AC于M,PN⊥DQ于N,则四边形PMDN是矩形,分别求解即可;
试题解析:(1)证明:如图1中,

∵∠EDE′=∠C=90°,∴∠ADP+∠CDE=90°,∠CDE+∠DEC=90°,
∴∠ADP=∠DEC.
(2)解:如图1中,当C′E′与AB相交于Q时,即![]() 时,过P作MN∥DC′,设∠B=α
时,过P作MN∥DC′,设∠B=α
∴MN⊥AC,四边形DC′MN是矩形,
∴PM=PQcosα=![]() y,PN=
y,PN=![]() ×
×![]() (3﹣x),
(3﹣x),
∴![]() (3﹣x)+
(3﹣x)+![]() y=x,∴
y=x,∴![]() ,
,
当DC′交AB于Q时,即![]() 时,如图2中,作PM⊥AC于M,PN⊥DQ于N,则四边形PMDN是矩形,
时,如图2中,作PM⊥AC于M,PN⊥DQ于N,则四边形PMDN是矩形,

∴PN=DM,
∵DM=![]() (3﹣x),PN=PQsinα=
(3﹣x),PN=PQsinα=![]() y,
y,
∴![]() (3﹣x)=
(3﹣x)=![]() y,∴
y,∴![]() .
.
综上所述, 
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4a2﹣25b2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2+mx+25能用完全平方公式分解因式,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
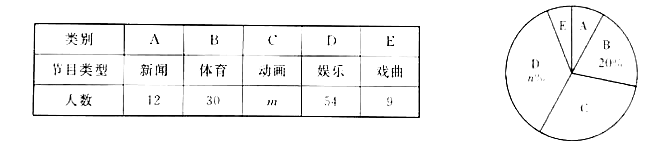
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,统计表中
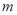 的值为 ,统计图中
的值为 ,统计图中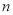 的值为 ;
的值为 ;(3)在统计图中,
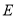 类所对应扇形圆心角的度数为 ;
类所对应扇形圆心角的度数为 ;(4)该校共有2000名学生,根据调查结果,估计该校最喜爱欣慰节目的学生数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:5x﹣3x=( )
A.2x
B.2x2
C.﹣2x
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
(1)如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
(2)如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
(3)当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知3x=6,3y=9,则32x﹣y= .
相关试题

