【题目】运用同底数幂的乘法法则计算.
(1)a4a3a2﹣a5a+a6a2a
(2)4×2n×2n-1(n>1)
参考答案:
【答案】
(1)
解答:a4a3a2﹣a5a+a6a2a
= a9﹣a6+a9
=2a9-a6
(2)
解答:原式=22×2n×2n-1
=22+n+n-1
=22n+1.
【解析】此题主要考查了同底数幂的乘法运算,正确掌握运算法则是解题关键.
【考点精析】利用同底数幂的乘法对题目进行判断即可得到答案,需要熟知同底数幂的乘法法则aman=am+n(m,n都是正数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(m-2)x2+2x+1=0有实数根,则m的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a2n-1an+5=a16 , 那么n=(n是整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学学习过程中,自学是一种非常重要的学习方式。通过自学不仅可以获得新知,而且可以培养和锻炼我们的思维品质。请你通过自学解答下面的问题:
(1)填空:有理数除法的符号法则是:两数相除,同号得正,异号得负.
例如:我们可以根据有理数除法的符号法则解不等式:
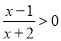 ,
,解:根据有理数除法的符号法则,有:
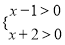 ,或
,或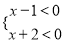
解得:
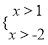 (1),或
(1),或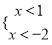 (2)
(2)由(1)得:
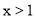 ,
,由(2)得:

所以,原不等式的解集为
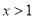 或
或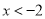 .
.问题:请用以上方法解不等式
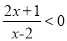 .
.(2)解决含有绝对值符号的问题,通常根据绝对值符号里所含式子的正负性,去掉绝对值符号,转化为不含绝对值符号的问题再解答.
例如:解不等式
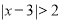 .
.解:①当
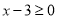 ,即
,即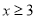 时,原式化为:
时,原式化为: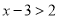 ,
,解得
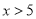 ,
,此时,不等式
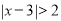 的解集为
的解集为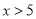 ;
;②当
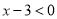 ,即
,即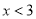 时,原式化为:
时,原式化为: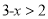 ,
,解得
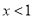 ,
,此时,不等式
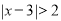 的解集为
的解集为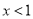 ;
;综上可知,原不等式的解集为
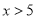 或
或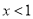 .
.问题:请用以上方法解不等式
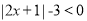 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白球”的频率折线统计图:

(1)请估计:当
 很大时,摸到白球的频率将会接近 (精确到0.01);假如你摸一次,你摸到白球的概率
很大时,摸到白球的频率将会接近 (精确到0.01);假如你摸一次,你摸到白球的概率 .
.(2)试估算盒子里白、黑两种颜色的球各有多少只?
(3)在(2)条件下如果要使摸到白球的概率为
 ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球? -
科目: 来源: 题型:
查看答案和解析>>【题目】星辰书店老板去图书批发市场购买某种图书.第一次用600元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的进价已比第一次提高了20%,老板用750元所购该书数量比第一次多5本.
(1)求第一次购书的进价;
(2)当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个圆柱形容器高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 ______ m(容器厚度忽略不计).

相关试题

