Question

【题目】如图，已知抛物线y=－x2+mx+3与x轴交于点A、B两点，与y轴交于C点，点B的坐标为（3，0），抛物线与直线y=－x+3交于C、D两点．连接BD、AD．

（1）求m的值．

（2）抛物线上有一点P，满足S△ABP=4S△ABD，求点P的坐标．

Answer 1

【答案】（1）m=2 （2）P（1+，－9）或P（1－，－9）

【解析】试题分析：（1）利用待定系数法即可解决问题；

（2）利用方程组首先求出点D坐标．由面积关系，推出点P的纵坐标，再利用待定系数法求出点P的坐标即可.

试题解析：（1）∵抛物线y=-x2+mx+3过（3，0），

∴0=-9+3m+3，

∴m=2

（2）由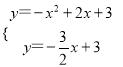，得， ，

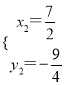∴D（，-），

∵S△ABP=4S△ABD，

∴AB×|yP|=4×AB×，

∴|yP|=9，yP=±9，

当y=9时，-x2+2x+3=9，无实数解，

当y=-9时，-x2+2x+3=-9，解得：x1=1+，x2=1-，

∴P（1+，-9）或P（1-，-9）．