【题目】已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为 
参考答案:
【答案】n> ![]() 或-1<n<3
或-1<n<3
【解析】解:当y=0时,y=x2-2x-3=0,(x-3)(x+1)=0,
x=-1或3,
∴A(-1,0),B(3,0),
y=x2-2x-3=(x-1)2-4,
∴M(1,-4),
如图,作直线y=-x,
分别过A、B作直线y=-x的平行线,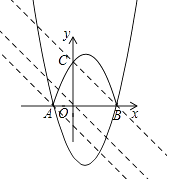
当直线y=-x+n经过A(-1,0)时,1+n=0,n=-1,
当直线y=-x+n经过B(3,0)时,-3+n=0,n=3,
∴n的取值范围为:-1<n<3,
根据题意得:翻折后的顶点坐标为(1,4),
∴翻折后的抛物线的解析式为:y=-(x-1)2+4=-x2+2x+3,
当直线y=-x+n与抛物线y=-x2+2x+3只有一个公共点时,
则 ![]() ,
,
-x2+2x+3=-x+n,
-x2+3x+3-n=0,
△=9+4(3-n)=0,
n= ![]() ,
,
综上所述:当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n> ![]() 或-1<n<3.
或-1<n<3.
【考点精析】掌握二次函数图象的平移和抛物线与坐标轴的交点是解答本题的根本,需要知道平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
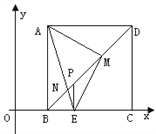
查看答案和解析>>【题目】如图,四边形ABCD位于平面直角坐标系的第一象限,B、C在x轴上A点函数
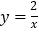 上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0)。
上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0)。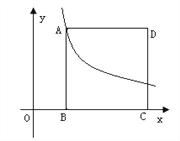
⑴试判断四边形ABCD的形状。
⑵如图若点P是线段BD上一点PE⊥BC于E,M是PD的中点,连EM、AM。
求证:AM=EM
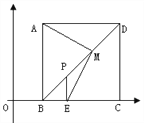
⑶在图中,连结AE交BD于N,则下列两个结论:
①
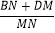 值不变;②
值不变;②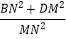 的值不变。其中有且仅有一个是正确的,请选择正确的结论证明并求其值。
的值不变。其中有且仅有一个是正确的,请选择正确的结论证明并求其值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线
 相交于点
相交于点 于点
于点 于点F,连结
于点F,连结 ,则下列结论:
,则下列结论: ;
; ;
; ;
; 图中共有四对全等三角形
图中共有四对全等三角形 其中正确结论的个数是
其中正确结论的个数是

A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交BC于点E,过点A作直线CD的垂线交CD于点F,若
 ,则
,则 的值为______.
的值为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)x(x-1)=3x+7
(2)4x2-4x+1=(x+3)2 -
科目: 来源: 题型:
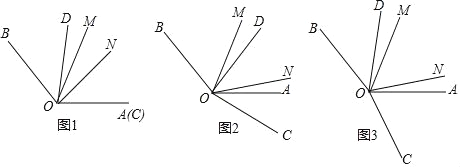
查看答案和解析>>【题目】已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.
(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,
①∠MON与旋转度数n°有怎样的数量关系?说明理由;
②当n为多少时,∠MON为直角?
(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OC绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
 请你根据上图填写下表:
请你根据上图填写下表:销售公司
平均数
方差
中位数
众数
甲
9
乙
9

8
 请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析: 从平均数和方差结合看;
从平均数和方差结合看; 从折线图上甲、乙两个汽车销售公司销售数量的趋势看
从折线图上甲、乙两个汽车销售公司销售数量的趋势看 分析哪个汽车销售公司较有潜力
分析哪个汽车销售公司较有潜力 .
.
相关试题

