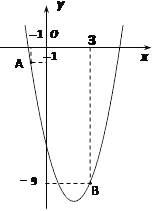
【题目】如图,已知二次函数![]() 的图像经过点A(-1,-1)和点B(3,-9).
的图像经过点A(-1,-1)和点B(3,-9).
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
参考答案:
【答案】(1)y=x2﹣4x﹣6;(2)对称轴为x=2;顶点坐标为(2,﹣10);(3)m=6,点Q到x轴的距离为46.
【解析】试题分析:(1)利用待定系数法确定二次函数的解析式;
(2)把(1)中得到的解析式配成顶点式,然后根据二次函数的性质确定顶点坐标和对称轴.
(3)将P(m,m)坐标代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6,解方程求得m的值,根据题意得到m=6,从而求得P的坐标,根据点P与点Q关于对称轴x=2对称,所以点Q到x轴的距离为6.
解:(1)将A(﹣1,﹣1)和点B(3,﹣9)代入y=ax2﹣4x+c,
得![]() 解得
解得![]() ,
,
所以二次函数的表达式为y=x2﹣4x﹣6;
(2)由y=x2﹣4x﹣6=(x﹣2)2﹣10可知:
对称轴为x=2;顶点坐标为(2,﹣10);
(3)将P(m,m)坐标代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6.
解得m1=﹣1,m2=6.
因为m>0,所以m=﹣1不合题意,舍去.所以m=6,
所以P点坐标为(6,6);
因为点P与点Q关于对称轴x=2对称,所以点Q到x轴的距离为46.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
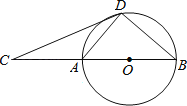
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若AB=6,tan∠CDA=
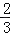 ,依题意补全图形并求DE的长.
,依题意补全图形并求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是计算机中的Excel电子表格,计算B2,C2,D2,E2和F2的和,其结果是( )
A
B
C
D
E
F
1
4
6
2
5
9
3
2
2
3
4
5
6
7
3
3
3
5
8
2
6
4
4
2
7
5
10
9
A. 28 B. 25 C. 15 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是以点O为圆心、AB为直径的半圆上的一个动点(点C不与点A、B重合),如果AB=4,过点C作CD⊥AB于D,设弦AC的长为x,线段CD的长为y,那么在下列图象中,能表示y与x函数关系的图象大致是( )
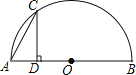
A.
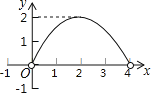 B.
B.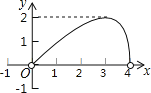
C.
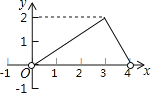 D.
D.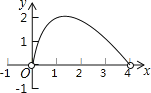
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:

(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= ;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列表述,能确定位置的是( )
A. 某电影院2排 B. 南京市大桥南路
C. 北偏东30° D. 东经118°,北纬40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保证中小学生每天锻炼一小时,涟水县某中学开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的统计图(1)和图(2).
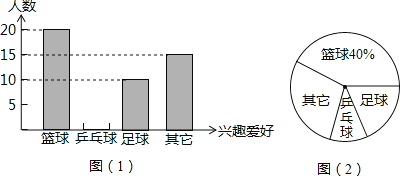
(1)某班同学的总人数为 人;
(2)请根据所给信息在图(1)中将表示“乒乓球”项目的图形补充完整;
(3)扇形统计图(2)中表示”篮球”项目扇形的圆心角度数为 .
相关试题

