【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
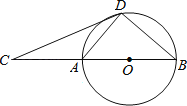
(1)求证:CD是⊙O的切线;
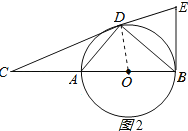
(2)过点B作⊙O的切线交CD的延长线于点E,若AB=6,tan∠CDA=![]() ,依题意补全图形并求DE的长.
,依题意补全图形并求DE的长.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)连OD,OE,根据圆周角定理得到∠ADO+∠1=90°,而∠CDA=∠CBD,∠CBD=∠1,于是∠CDA+∠ADO=90°;
(2)根据切线的性质得到ED=EB,OE⊥BD,则∠ABD=∠OEB,得到tan∠CDA=tan∠OEB=![]() =
=![]() ,易证Rt△CDO∽Rt△CBE,得到
,易证Rt△CDO∽Rt△CBE,得到![]() =
=![]() ,
,
求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长,由切线长定理即可得DE的长.
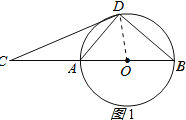
(1)证明:连OD,OE,如图1所示,
∵AB为直径,
∴∠ADB=90°,
即∠ADO+∠BDO=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠BDO,
∴∠BDO=∠CDA,
∴∠CDA+∠ADO=90°,
即∠CDO=90°,
∴CD⊥OD,
∴CD是⊙O的切线;
(2)解:如图2所示:
∵EB为⊙O的切线,
∴ED=EB,OE⊥DB,
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA=![]() ,
,
∴tan∠OEB=![]() =
=![]() ,
,
∵Rt△CDO∽Rt△CBE,
∴![]() =
=![]() ,
,
∴CD=![]() ×6=4,
×6=4,
在Rt△CBE中,设BE=x,
∴(x+4)2=x2+62,
解得:x=![]() .
.
即BE的长为![]() ,
,
∴DE=BE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方形的边长为5 cm,它的边长减少x(cm)后得到的新正方形的周长为y(cm).
(1)求y关于x的函数表达式.
(2)当x=2时,求y的值,并说明这个函数值的实际意义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果用(7,8)表示七年级八班,那么八年级七班可表示成______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各式中,与(a﹣b)2一定相等的是( )
A.a2+2ab+b2 B.a2﹣b2
C.a2+b2 D.a2﹣2ab+b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是计算机中的Excel电子表格,计算B2,C2,D2,E2和F2的和,其结果是( )
A
B
C
D
E
F
1
4
6
2
5
9
3
2
2
3
4
5
6
7
3
3
3
5
8
2
6
4
4
2
7
5
10
9
A. 28 B. 25 C. 15 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是以点O为圆心、AB为直径的半圆上的一个动点(点C不与点A、B重合),如果AB=4,过点C作CD⊥AB于D,设弦AC的长为x,线段CD的长为y,那么在下列图象中,能表示y与x函数关系的图象大致是( )
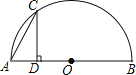
A.
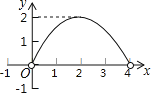 B.
B.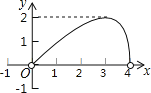
C.
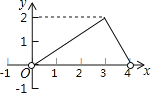 D.
D.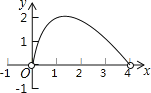
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
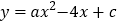 的图像经过点A(-1,-1)和点B(3,-9).
的图像经过点A(-1,-1)和点B(3,-9).(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
相关试题

