【题目】如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,求
,求![]() 的长度.
的长度.

参考答案:
【答案】(1)∠CFD=63°;(2)AD=![]()
【解析】
(1)根据三角形的内角和以及平行线的性质解答即可;
(2)勾股定理求出AC的长度,根据角平分线的性质得到DC=DE,证明Rt△BED≌Rt△BCD(HL),得到BE=BC=5,从而得出AE=8,设DE=DC=x,则AD=12-x,在Rt△ADE中利用勾股定理,列出方程解出x,即可求出AD.
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=36°,
∴∠ABC=90°-36°=54°,
∵BD平分∠ABC交AC于点D,
∴∠ABD=∠DBC=27°,
∴∠BDC=63°,
∵DE⊥AB,
∴∠ADE=90°-36°=54°,
∵CF∥BD,
∴∠DCF=∠BDC=63°.
∵∠CDF=∠ADE=54°,
∴∠CFD=180°∠DCF∠CDF=63°.
(2)∵在Rt△ABC中,AB=13,BC=5,
∴AC=![]() ,
,
∵BD平分∠ABC,∠C=90°,DE⊥AB,
∴DC=DE,
在Rt△BED与Rt△BCD中,
DE=DC,BD=BD,
∴Rt△BED≌Rt△BCD(HL)
∴BE=BC=5,
∴AE=13-5=8,
设DE=DC=x,
则AD=12-x,
在Rt△ADE中,AE2+DE2=AD2,即82+x2=(12-x)2,解得:x=![]() ,
,
∴AD=12-![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】向日葵水果店推出甲乙两种礼盒,甲礼盒中有樱桃
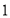 千克,枇杷
千克,枇杷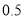 千克,香梨
千克,香梨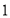 千克,乙礼盒中有樱桃
千克,乙礼盒中有樱桃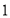 千克,枇杷
千克,枇杷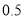 千克,哈蜜瓜
千克,哈蜜瓜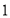 千克,己知樱桃每千克
千克,己知樱桃每千克 元,甲礼盒每盒
元,甲礼盒每盒 元,乙礼盒每盒
元,乙礼盒每盒 元,当然,顾客也可根据需要自由搭配,小陶用
元,当然,顾客也可根据需要自由搭配,小陶用 元买乙礼盒和自由搭配礼盒(香梨
元买乙礼盒和自由搭配礼盒(香梨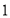 千克,枇杷
千克,枇杷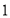 千克,哈蜜瓜
千克,哈蜜瓜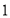 千克)若干盒,则小陶一共可买礼盒____个.
千克)若干盒,则小陶一共可买礼盒____个. -
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )

A. 4m厘米 B. 4n厘米 C. 2(m+n)厘米 D. 4(m-n)厘米
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分
频数
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
n
80≤x<90
m
0.35
90≤x≤100
50
0.25
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
 中,
中, ,对角线
,对角线 交于点
交于点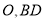 平分
平分 ,延长
,延长 至点
至点 ,使
,使 ,连接
,连接 .
.(1)求证:四边形
 是菱形;
是菱形;(2)若
 ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2(1﹣m)x+m2=0的两实数根为x1 , x2 , 则y=x1+x2+2x1x2的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 .
.(1)求直线
 的解析式;
的解析式;(2)把直线
 向右平移并与
向右平移并与 轴相交于
轴相交于 得到
得到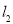 ,请在如图所示平面直角坐标系中作出直线
,请在如图所示平面直角坐标系中作出直线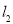 ;
;(3)若直线
 与
与 轴交于
轴交于 点,与直线
点,与直线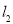 交于点
交于点 ,求
,求 的面积.
的面积.
相关试题

