【题目】如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为![]() , Rt△BFC的面积为
, Rt△BFC的面积为![]() , Rt△DCE的面积为
, Rt△DCE的面积为![]() , 则
, 则![]() _______
_______ ![]() (用“>”、“=”、“<”填空);
(用“>”、“=”、“<”填空);
(2)写出图中的三对相似三角形,并选择其中一对进行证明.

参考答案:
【答案】(1)=;(2)证明见解析.
【解析】试题分析:(1)、根据题意得出三个面积之间的关系;(2)、△BCD∽△CFB∽△DEC,根据同角的余角相等得出∠EDC=∠CBD,然后根据垂直得出三角形相似.
试题解析:(1)、![]() .
.
(2)、△BCD∽△CFB∽△DEC.
可任选一对,如:△BCD∽△DEC;
∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,∴△BCD∽△DEC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AB上有一点P,点M、N分别为线段PA、PB的中点,AB=14.
(1)若点P在线段AB上,且AP=8,求线段MN的长度;
(2)若点P在直线AB上运动,设AP=x,BP=y,请分别计算下面情况时MN的长度: ①当P在AB之间(含A或B);
②当P在A左边;
③当P在B右边;你发现了什么规律?
(3)如图2,若点C为线段AB的中点,点P在线段AB的延长线上,下列结论:① 的值不变;②
的值不变;②  的值不变,请选择一个正确的结论并求其值.
的值不变,请选择一个正确的结论并求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工人若每小时生产38个零件,在规定时间内还有15个不能完成,若每小时生产42个零件,则可以超额完成5个,问:规定时间是多少?设规定时间为x小时,则可列方程为( )
A. 38x﹣15=42x+5 B. 38x+15=42x﹣5 C. 42x+38x=15+5 D. 42x﹣38x=15﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形的四个顶点在同一圆上,则该平行四边形一定是( )
A.正方形
B.菱形
C.矩形
D.等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.
B.(﹣2)3=8
C.﹣|﹣3|=3
D.﹣22=﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
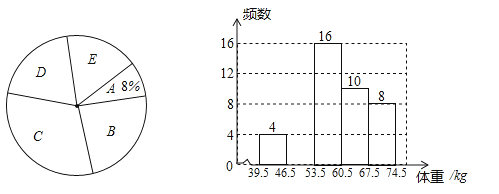
解答下列问题:
(1)这次抽样调查的样本容量是 并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有 名? -
科目: 来源: 题型:
查看答案和解析>>【题目】在3张正面分别写有数字﹣2,﹣1,0的卡片,它们的背面完全相同,现将这3张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不大于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为a的值,然后再从剩余的卡片随机抽一张,以其正面的数字作为b的值,请用列表法或画树状图法,求点Q(a,b)在第三象限的概率.
相关试题

