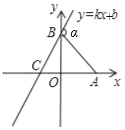
【题目】如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
根据等腰直角三角形的性质和三角函数分别求B、C两点的坐标,利用待定系数法求直线的表达式.
∵A点坐标为(5,0),
∴OA=5,
∵∠BCA=60°,∠α=105°,
∴∠BAC=105°﹣60°=45°,
∴△AOB是等腰直角三角形,
∴AO=BO=5,
∴B(0,5).
∵∠CBO=90°﹣∠BCA=30°,
∴BC=2CO,BO=![]() =
=![]() CO=5,
CO=5,
∴CO=![]() ,
,
∴C(﹣![]() ,0),
,0),
把B(0,5)和C(﹣![]() ,0)代入y=kx+b中得:
,0)代入y=kx+b中得: ,
,
解得: ,
,
∴直线BC的表达式为:y=![]() x+5.
x+5.
故选:B.
-
科目: 来源: 题型:
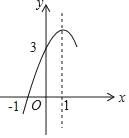
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大;
其中结论正确有_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=
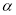 ,△BOC≌△ADC,∠OCD=60°,连接OD.
,△BOC≌△ADC,∠OCD=60°,连接OD.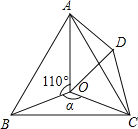
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试求证:△AOD是直角三角形;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足
 +(c-7)2=0.
+(c-7)2=0.(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根 长为 1 米的竹竿的影长为 0.4 米,同时另一名同学测量树的高度时, 发现树的影子不全落在地面上,有一部分落在教学楼的第一级台 阶水平面上,测得此影子长为 0.2 米,一级台阶高为 0.3 米,如图 所示,若此时落在地面上的影长为 4.4 米,则树高为( )

A.11.8 米B.11.75 米
C.12.3 米D.12.25 米
-
科目: 来源: 题型:
查看答案和解析>>【题目】进入夏季用电高峰季节,市供电局维修队接到紧急通知:要到 30 千米远的某乡镇进行紧急抢修,维修工骑摩托车先走,15 分钟后,抢修车装载所需材料出发, 结果两车同时到达抢修点,已知抢修车的速度是摩托车速度的 1.5 倍,求两种车的速 度.
-
科目: 来源: 题型:
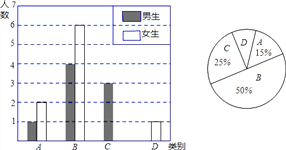
查看答案和解析>>【题目】我县实施新课程改革后,学生的自主学习、合作交流能力有很大提高,胡老师为了了解班级学生自主学习、合作交流的具体情况,对某班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,胡老师一共调查了 名同学,其中女生共有 ___名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,胡老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
相关试题

