【题目】已知,如图△ABC中,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE.
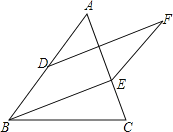
(1)猜想:DF与AE的关系是 ;
(2)试说明你猜想的正确性.
参考答案:
【答案】(1)DF与AE互相平分;(2)证明见解析
【解析】
试题分析:(1)DF与AE互相平分.
(2)由已知可得四边形BDFE是平行四边形,从而可得BD=EF,由中点的定义可得AD=BD,再根据平行线的性质即可得到∠ADO=∠EFO,∠DAO=∠FEO,从而可利用ASA判定△ADO≌△EFO,根据全等三角形的对应边相等即可得到OD=OF,OA=OE,即得到AE与DF互相平分,或连接AF、DE,然后证明四边形DEFA是平行四边形,再根据平行四边形的对角线互相平分证明.
解:(1)DF与AE互相平分;
∵D是AB的中点,
∴AD=BD,
∵EF∥AB,DF∥BE,
∴四边形BEFD是平行四边形,
∴EF=BD=AD,
∵EF∥AB,
∴EF∥AD,
∵EF∥AD,EF=AD,
∴四边形AFED是平行四边形,
∴DF、AE是平行四边形AFED的对角线,
∴DF、AE互相平分;
(2)∵EF∥AB,DF∥BE,
∴四边形BDFE是平行四边形,
∴BD=EF,
∵D是AB的中点,
∴AD=BD,
∴EF=AD,
∵EF∥AB,
∴∠ADO=∠EFO,∠DAO=∠FEO,
在△ADO和△EFO中,
∵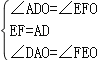 ,
,
∴△ADO≌△EFO,
∴OD=OF,OA=OE,
即AE与DF互相平分;
或连接AF、DE.
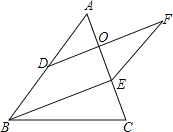
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个样本﹣1,0,2,x,3,它们的平均数是2,则x=_____,方差S2=_____。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等式2a□a=2a2一定成立,则□内的运算符号为( )
A.+ B.﹣ C.× D.÷
-
科目: 来源: 题型:
查看答案和解析>>【题目】长春市地铁1号线预计今年9月份通车,线路总长约为18500m.数据18500用科学记数法表示是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣3x+1=0的根的判别式的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若定义:f(a,b)=(-a,b),g(m,n)=(m,-n),例如f(1,2)=(-1,2),g(-4,-5)=(-4,5),则g(f(2,-3))=( )
A. (2,-3) B. (-2,3) C. (2,3) D. (-2,-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把命题“实数是无理数”改成“如果……,那么……”的形式:____________,它是个____________命题.(填“真”或“假” )
相关试题

