【题目】如图所示,学校内有一块四边形的空地ABCD,现计划在该空地上种植草坪经测量,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草坪皮需要400元,问需要投入多少元?

参考答案:
【答案】14400(元).
【解析】
仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解
解:连接BD,
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在△CBD中,CD2=132,BC2=122,
而122+52=132,
即BC2+BD2=CD2,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=![]() ADAB+
ADAB+![]() DBBC,
DBBC,
=![]() ×4×3+
×4×3+![]() ×12×5=36.
×12×5=36.
所以需费用36×400=14400(元).

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
①(x+1)(x﹣1)﹣(x﹣2)2,其中x=
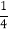 .
.②[(x+y)2﹣y(2x+y)﹣8xy]÷2x,其中x=2,
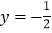 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2x、宽为2y的长方形,沿图中虚线用剪刀剪成四个完全相同的小长方形,然后按图2所示拼成一个正方形.

(1)你认为图2中的阴影部分的正方形的边长等于
(2)试用两种不同的方法求图2中阴影部分的面积.
方法1: 方法2:
(3)根据图2你能写出下列三个代数式之间的等量关系吗?
代数式:(x+y)2,(x-y)2,4xy.(4)根据(3)题中的等量关系,解决如下问题:
若x+y=4,xy=3,则(x-y)2= -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
-
科目: 来源: 题型:
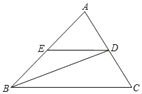
查看答案和解析>>【题目】如图,已知△ABC中,AB=BC,D为AC中点,过点D作DE∥BC,交AB于点E.
(1)求证:AE=DE;
(2)若∠C=65°,求∠BDE的度数.
-
科目: 来源: 题型:
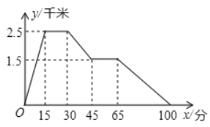
查看答案和解析>>【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在Rt△ABC中,∠BAC=
 ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
相关试题

