【题目】已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红的年龄的![]() 还多1岁.
还多1岁.
(1)请用含m的式子表示这三人的年龄和;
(2)若这三人的年龄和为35岁,请你求出这三人的年龄.
参考答案:
【答案】(1)4m﹣5;(2)小明的年龄是10岁,小红的年龄是16岁,小华的年龄是9岁.
【解析】试题分析:(1)根据题意分别列出小明、小红和小华的年龄,再相加,去括号,合并同类项,即可求出这三名同学的年龄的和;
(2)根据题意可得关于m的方程,解方程求出m的值,再分别求出各自的年龄即可.
试题解析:(1)∵小明的年龄是m岁,
∴小红的年龄为(2m﹣4)岁,小华的年龄为[![]() (2m﹣4)+1]岁,
(2m﹣4)+1]岁,
∴三人的年龄和为:m+(2m﹣4)+![]() (2m﹣4)+1=m+2m﹣4+m﹣2+1=4m﹣5;
(2m﹣4)+1=m+2m﹣4+m﹣2+1=4m﹣5;
(2)根据题意得:4m﹣5=35,
解得:m=10,
∴2m﹣4=16,![]() (2m﹣4)+1=9,
(2m﹣4)+1=9,
答:小明的年龄是10岁,小红的年龄是16岁,小华的年龄是9岁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
(1)如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D______(A,B)的好点,但点D______(B,A)的好点.(请在横线上填是或不是)知识运用:
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为-2.数______所表示的点是(M,N)的好点;
(3)如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过______秒时,P、A和B中恰有一个点为其余两点的好点?
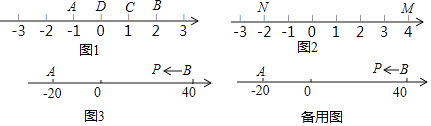
-
科目: 来源: 题型:
查看答案和解析>>【题目】某月份的日历表如图.任意圈出一横行或一竖列相邻的三个数.这三个数的和不可能是( )

A. 24 B. 42 C. 58 D. 66
-
科目: 来源: 题型:
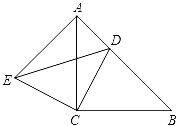
查看答案和解析>>【题目】如图,D为AB上一点,△ACE≌△BCD,AD2+DB2=DE2,试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).

(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求经过点C的反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,2秒后,两点相距16个单位长度,已知点B的速度是点A的速度的3倍,(速度单位:单位长度/秒)
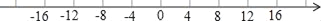
(1)求出点A、B运动的速度,并在数轴上标出A、B两点从原点出发运动2秒时的位置;
(2)若A、B两点从(1)中标出的位置开始,仍以原来的速度同时沿数轴向左运动,第t秒后,
①点A在数轴上的位置表示的数为 ;点B在数轴上的位置表示的数为 ;(用含t的代数式表示)
②当t为多少时,点A、B之间相距4个单位长度?
-
科目: 来源: 题型:
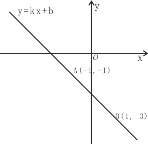
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点A(1,1)和点B(1,3).求:
(1)求一次函数的表达式;
(2)求直线AB与坐标轴围成的三角形的面积;
(3)请在x轴上找到一点P,使得PA+PB最小,并求出P的坐标.
相关试题

