【题目】已知:如图,AC⊥BC,CD∥FG,∠1=∠2,试说明:DE⊥AC.
参考答案:
【答案】证明:∵CD∥FG,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DE∥BC,
∵AC⊥BC,
∴DE⊥AC.
【解析】首先依据平行线的性质可证明∠2=∠DCB,然后通过等量代换得∠DCB=∠1,接下来,依据内错角相等两直线平行可得到DE∥BC,最后,依据利用平行线的性质得出结论即可.
【考点精析】关于本题考查的垂线的性质和平行线的判定与性质,需要了解垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
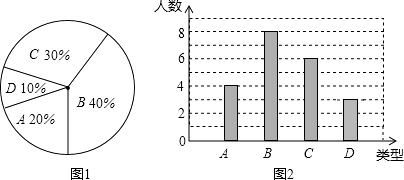
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:
①小宇的分析是从哪一步开始出现错误的?
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵. -
科目: 来源: 题型:
查看答案和解析>>【题目】若xm-2-4y2n+1=5是关于x,y的二元一次方程,则m=_______,n=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
 与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图
趣题巧解
数学应用
魔方复原
甲
66
89
86
68
乙
66
60
80
68
丙
66
80
90
68
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的补角是150°,那么这个角的余角的度数是( )
A.30°
B.60°
C.90°
D.120° -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(x﹣2)2+1的顶点坐标是 .
相关试题

