【题目】如图1,抛物线![]() 与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
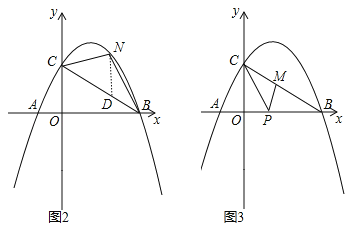
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)m=1,n=﹣9;(2)![]() ;(3)P(
;(3)P(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
试题分析:(1)∵抛物线的解析式为![]() =
=![]() ,∴抛物线的对称轴为直线x=2,∵点A和点B为对称点,∴2﹣(m﹣2)=2m+3﹣2,解得m=1,∴A(﹣1,0),B(5,0),把A(﹣1,0)代入
,∴抛物线的对称轴为直线x=2,∵点A和点B为对称点,∴2﹣(m﹣2)=2m+3﹣2,解得m=1,∴A(﹣1,0),B(5,0),把A(﹣1,0)代入![]() 得9+n=0,解得n=﹣9;
得9+n=0,解得n=﹣9;
(2)作ND∥y轴交BC于D,如图2,抛物线解析式为![]() =
=![]() ,当x=0时,y=3,则C(0,3),设直线BC的解析式为y=kx+b,把B(5,0),C(0,3)代入得
,当x=0时,y=3,则C(0,3),设直线BC的解析式为y=kx+b,把B(5,0),C(0,3)代入得![]() ,解得:
,解得: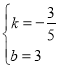 ,∴直线BC的解析式为
,∴直线BC的解析式为![]() ,设N(x,
,设N(x,![]() ),则D(x,
),则D(x,![]() ),∴ND=
),∴ND=![]() =
=![]() ,∴S△NBC=S△NDC+S△NDB=
,∴S△NBC=S△NDC+S△NDB=![]() 5ND=
5ND=![]() =
=![]() ,当x=
,当x=![]() 时,△NBC面积最大,最大值为
时,△NBC面积最大,最大值为![]() ;
;
(3)存在.
∵B(5,0),C(0,3),∴BC=![]() =
=![]() ;分两种情况讨论:
;分两种情况讨论:
①当∠PMB=90°,则∠PMC=90°,△PMC为等腰直角三角形,MP=MC,设PM=t,则CM=t,MB=![]() ﹣t,∵∠MBP=∠OBC,∴△BMP∽△BOC,∴
﹣t,∵∠MBP=∠OBC,∴△BMP∽△BOC,∴![]() ,即
,即![]() ,解得t=
,解得t=![]() ,BP=
,BP=![]() ,∴OP=OB﹣BP=5﹣
,∴OP=OB﹣BP=5﹣![]() =
=![]() ,此时P点坐标为(
,此时P点坐标为(![]() ,0);
,0);
②当∠MPB=90°,则MP=MC,设PM=t,则CM=t,MB=![]() ﹣t,∵∠MBP=∠CBO,∴△BMP∽△BCO,∴
﹣t,∵∠MBP=∠CBO,∴△BMP∽△BCO,∴![]() ,即
,即![]() ,解得t=
,解得t=![]() ,BP=
,BP=![]() ,∴OP=OB﹣BP=5﹣
,∴OP=OB﹣BP=5﹣![]() =
=![]() ,此时P点坐标为(
,此时P点坐标为(![]() ,0);
,0);
综上所述,P点坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
-
科目: 来源: 题型:
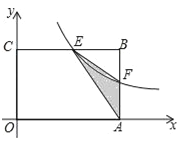
查看答案和解析>>【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数
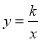 (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
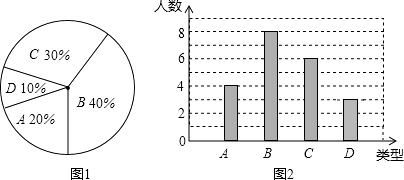
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:
①小宇的分析是从哪一步开始出现错误的?
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵. -
科目: 来源: 题型:
查看答案和解析>>【题目】若xm-2-4y2n+1=5是关于x,y的二元一次方程,则m=_______,n=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AC⊥BC,CD∥FG,∠1=∠2,试说明:DE⊥AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图
趣题巧解
数学应用
魔方复原
甲
66
89
86
68
乙
66
60
80
68
丙
66
80
90
68
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的补角是150°,那么这个角的余角的度数是( )
A.30°
B.60°
C.90°
D.120°
相关试题

