【题目】分别用 ![]() ,
,![]() ,
,![]() ,
,![]() 表示有理数,
表示有理数,![]() 是最小的正整数,
是最小的正整数,![]() 是最大的负整数,
是最大的负整数,![]() 是绝对值最小的有理数,
是绝对值最小的有理数,![]() 是数轴上到原点距离为
是数轴上到原点距离为![]() 的点表示的数;
的点表示的数;
(1)直接写出 ![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() 的倒数.
的倒数.
参考答案:
【答案】(1)a=1,b=-1,c=0,d=3或-3;(2)![]() 或
或![]()
【解析】
(1)根据有理数的相关概念可直接确定a、b、c、d的值;
(2)分情况求![]() 的值,然后再求其倒数即可.
的值,然后再求其倒数即可.
解:(1)∵![]() 是最小的正整数,
是最小的正整数,![]() 是最大的负整数,
是最大的负整数,![]() 是绝对值最小的有理数,
是绝对值最小的有理数,![]() 是数轴上到原点距离为
是数轴上到原点距离为![]() 的点表示的数,
的点表示的数,
∴a=1,b=-1,c=0,d=3或-3;
(2)当d=3时,4a+3b+2c+d=4×1+3×(1)+2×0+3=4,
所以4a+3b+2c+d的倒数是![]() ;
;
当d=3时,4a+3b+2c+d=4×1+3×(1)+2×03=2,
所以4a+3b+2c+d的倒数是:![]() ,
,
综上所述:4a+3b+2c+d的倒数是:![]() 或
或![]() .
.
-
科目: 来源: 题型:
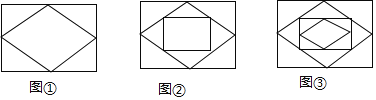
查看答案和解析>>【题目】已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形.如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第3个图形中直角三角形的个数有______个,第2018个图形中直角三角形的个数有______个.
-
科目: 来源: 题型:
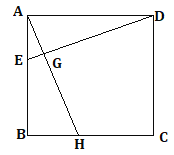
查看答案和解析>>【题目】如图,点E、H分别在正方形ABCD的边AB、BC上,且AE=BH
求证:(1)DE=AH (2)DE⊥AH
-
科目: 来源: 题型:
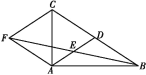
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的条件下,要使四边形ADCF为正方形,在△ABC中应添加什么条件,请直接把补充条件写在横线上 (不需说明理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于50%.经试销发现,销售量P(件)与销售单价x(元)符合一次函数关系,当销售单价为65元时销售量为55件,当销售单价为75元时销售量为45件.
(Ⅰ)求P与x的函数关系式;
(Ⅱ)若该商场获得利润为y元,试写出利润y与销售单价x之间的关系式;
(Ⅲ)销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
-
科目: 来源: 题型:
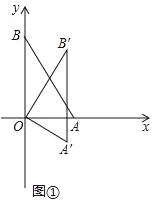
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点A(1,0),点B(0,
 ),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.
),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.(Ⅰ)如图①,当α=30°时,求点B′的坐标;
(Ⅱ)设直线AA′与直线BB′相交于点M.
如图②,当α=90°时,求点M的坐标;
②点C(﹣1,0),求线段CM长度的最小值.(直接写出结果即可)
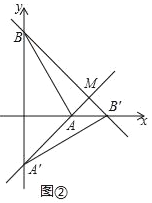
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,
 的顶点均在格点上,点
的顶点均在格点上,点 的坐标为
的坐标为 .
.
①把
 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的 ,画出
,画出 ,并写出
,并写出 的坐标;
的坐标;②以原点
 为对称中心,画出
为对称中心,画出 与关于原点
与关于原点 对称的
对称的 ,并写出点
,并写出点 的坐标.
的坐标.③以原点O为旋转中心,画出把
 顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
相关试题

