【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D,C分别在M,N的位置上,若∠EFG=56°,则∠1= , ∠2= . 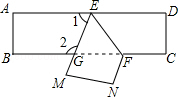
参考答案:
【答案】68°;112°
【解析】解:∵一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D,C分别在M,N的位置上, ∴∠MEF=∠FED,∠EFC+∠GFE=180°,
∵AD∥BC,∠EFG=56°,
∴∠FED=∠EFG=56°,
∵∠1+∠GEF+∠FED=180°,
∴∠1=180°﹣56°﹣56°=68°,
又∵∠1+∠2=180°,
∴∠2=180°﹣68°=112°.
故答案为:68°,112°.
首先根据折叠的性质和平行线的性质求∠FED的度数,然后根据三角形内角和定理求出∠1的度数,最后根据平行线的性质求出∠2的度数.
-
科目: 来源: 题型:
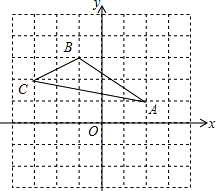
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(4,-3)所在象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ax2﹣2ax+a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成证明并写出推理根据: 已知,如图,∠1=132°,∠ACB=48°,∠2=∠3,FH⊥AB于H.
求证:CD⊥AB.
证明:∵∠1=132°,∠ACB=48°,
∴∠1+∠ACB=180°
∴DE∥BC
∴∠2=()
又∵∠2=∠3
∴∠3=∠DCB
∴HF∥()
∴∠CDB= . ()
又∵FH⊥AB,
∴∠FHB=()
∴∠CDB=°.
∴CD⊥AB.()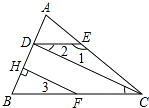
-
科目: 来源: 题型:
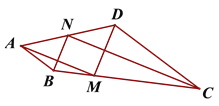
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=150°,∠BCD=30°,点M在BC上,AB=BM,CM=CD,点N为AD的中点,求证:BN⊥CN。
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年,我县冬天某天的气温是﹣1℃~4℃,这一天的温差是____.
相关试题

